2022-2023学年浙南名校联盟高二（下）期末数学试卷

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|（x+1）（x-2）＜0}，B={x|2^x-1≥1}，则A∩B=（　　）

  A．（1，2）

  B．[1，2）

  C．（-1，2）

  D．（0，2）
  组卷：1引用：2难度：0.7

  解析

• 2．已知复数z满足（1+2i）z=4+3i,则复数z的实部和虚部之和为（　　）

  A．3

  B． 5

  C．1

  D．-1
  组卷：5引用：2难度：0.9

  解析

• 3．已知m,n是两条不同的直线，α是一个平面，则下列命题是真命题的为（　　）

  A．若m∥n,n⊂α，则m∥α

  B．若m⊥α，m∥n,则n⊥α

  C．若m∥α，n∥α，则m∥n

  D．若α⊥β，α∩β=m,n⊥m,则n⊥α
  组卷：39引用：3难度：0.7

  解析

• 4．已知

  a

  =

  （

  1

  ，

  x

  ）

  ，

  b

  =

  （

  3

  ，-

  4

  ）

  ，若向量

  a

  在向量

  b

  上的投影向量为

  （

  -

  3

  5

  ，

  4

  5

  ）

  ，则x=（　　）

  A．2

  B．-2

  C．1

  D．-1
  组卷：12引用：1难度：0.7

  解析

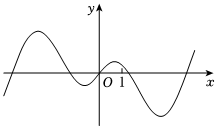• 5．已知函数f（x）的部分图象如图所示，则f（x）可能为（　　）

  A． f （ x ） = sinx + ln （ x + x 2 + 1 ）	B． f （ x ） = sinx • ln （ x + x 2 + 1 ）
  C． f （ x ） = cosx + ln （ x + x 2 + 1 ）	D． f （ x ） = cosx • ln （ x + x 2 + 1 ）
  组卷：9引用：2难度：0.8

  解析

• 6．已知直线y=ax+b与函数f（x）=xlnx相切，则

  1

  -

  a

  b

  （　　）

  A．有最大值e	B．有最小值-e
  C．有最大值 1 e	D．有最小值 - 1 e
  组卷：13引用：2难度：0.7

  解析

• 7．过点G（2，2）作两条直线分别交抛物线y²=2x于A，B两点，记直线GA，GB的斜率分为k₁，k₂，若k₁+k₂=5，k₁•k₂=-2，则直线AB的方程为（　　）

  A．2x+9y+12=0	B．2x-9y-12=0
  C．4x+18y+13=0	D．4x-18y-13=0
  组卷：11引用：2难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  离心率为2，A₁，A₂分别是左、右顶点，点M是直线x=1上一点，且满足3tan∠MA₁A₂=tan∠MA₂A₁，直线MA₁，MA₂分别交双曲线右支于B，C两点．记△MA₁A₂，△MBC的面积分别为S₁，S₂．
  （1）求双曲线C的方程；
  （2）求

  S

  1

  S

  2

  的最大值．
  组卷：15引用：3难度：0.2

  解析

• 22．已知函数f（x）=e^x（2x²-x-1）．
  （1）求f（x）的单调区间；
  （2）若g（x）=|f（x）|-a（a＞0）有3个不同的零点x₁＜x₂＜x₃．
  （ⅰ）求实数a的取值范围；
  （ⅱ）求证：x₂+x₃＜2．
  组卷：10引用：2难度：0.4

  解析