2023-2024学年山东省泰安市新泰市弘文中学高二(上)第一次月考数学试卷
发布:2024/9/15 16:0:8
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.已知直线l经过点A(1,3),B(5,7),则l的倾斜角为( )
组卷:134引用:5难度:0.9 -
2.满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
组卷:178引用:11难度:0.9 -
3.过点P(
,-23)且倾斜角为135°的直线方程为( )3组卷:1671引用:28难度:0.7 -
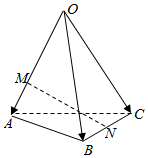 4.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9
4.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9 -
5.已知P是平面ABCD所在平面外一点,如果
=(2,-1,-4),AB=(4,2,0),AD=(-1,2,-1),则下列结论中错误的是( )AP组卷:23引用:2难度:0.8 -
6.已知点A(2,-3),B(-3,-2),直线l过点(1,1)且与线段AB相交,则直线l的斜率的范围是( )
组卷:216引用:10难度:0.7 -
 7.如图,二面角α-AB-β的大小为θ,P,Q分别在平面α,β内,PM⊥AB,NQ⊥AB,|PM|=m,|QN|=n,|PQ|=l,则|MN|=( )组卷:331引用:4难度:0.5
7.如图,二面角α-AB-β的大小为θ,P,Q分别在平面α,β内,PM⊥AB,NQ⊥AB,|PM|=m,|QN|=n,|PQ|=l,则|MN|=( )组卷:331引用:4难度:0.5
四、解答题(本大题共6小题,第17-18题每小题10分,第19-21题每小题10分,第22题14分,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
-
 21.如图,在三棱柱ABC-A1B1C1中,AB=BC,AC=AA1,点D为棱AC的中点,平面ABC⊥平面AA1C1C,且∠A1AC=60°.
21.如图,在三棱柱ABC-A1B1C1中,AB=BC,AC=AA1,点D为棱AC的中点,平面ABC⊥平面AA1C1C,且∠A1AC=60°.
(1)求证:A1D⊥平面ABC;
(2)若AB⊥BC,求二面角D-B1C-B的正弦值.组卷:436引用:11难度:0.4 -
 22.在如图所示的几何体中,四边形ABCD为矩形,AF⊥平面ABCD,EF∥AB,AD=2,AB=AF=2EF=1,点P为棱DF的中点.
22.在如图所示的几何体中,四边形ABCD为矩形,AF⊥平面ABCD,EF∥AB,AD=2,AB=AF=2EF=1,点P为棱DF的中点.
(1)求证:BF∥平面APC;
(2)求直线DE与平面BCF所成角的正弦值;
(3)求点E到平面BCF的距离.组卷:56引用:2难度:0.5


