2023-2024学年湖北省武汉市江夏区光谷实验中学九年级（上）国庆检测数学试卷

一、选择题（每小题3分，共30分）

• 1．将一元二次方程5x²-1=4x化成一般形式后，二次项的系数和一次项系数分别是（　　）

  A．5，-1

  B．5，4

  C．5，-4

  D．5，1
  组卷：1539引用：39难度：0.9

  解析

• 2．用配方法解方程x²-4x-3=0．下列变形正确的是（　　）

  A．（x-4）2=19

  B．（x-2）2=7

  C．（x-2）2=1

  D．（x+2）2=7
  组卷：560引用：18难度：0.7

  解析

• 3．下列关于x的一元二次方程中，有两个不相等的实数根的方程是（　　）

  A．x2+4=0

  B．4x2-4x+1=0

  C．x2+x+3=0

  D．x2+2x-1=0
  组卷：189引用：22难度：0.9

  解析

• 4．一元二次方程x²-3x+2=0的两根分别是x₁、x₂，则x₁+x₂的值是（　　）

  A．3

  B．2

  C．-3

  D．-2
  组卷：343引用：18难度：0.9

  解析

• 5．在同一平面直角坐标系中，函数y=ax²+k与y=kx+a（a≠0）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1932引用：15难度：0.5

  解析

• 6．若将抛物线y=2x²向上平移3个单位，所得抛物线的解析式为（　　）

  A．y=2x2+3

  B．y=2x2-3

  C．y=2（x-3）2

  D．y=2（x+3）2
  组卷：117引用：11难度：0.7

  解析

• 7．某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是13，则每个支干长出（　　）

  A．2根小分支

  B．3根小分支

  C．4根小分支

  D．5根小分支
  组卷：1177引用：15难度：0.7

  解析

• 8．已知二次函数y=ax²-2ax+1（a＜0）图象上三点A（-1，y₁），B（2，y₂）C（4，y₃），则y₁、y₂、y₃的大小关系为（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y1＜y3＜y2

  D．y3＜y1＜y2
  组卷：4801引用：9难度：0.5

  解析

三、解答题：（共8题，共72分）

• 23．（1）问题背景．
  如图1，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是线段BC、线段CD上的点．若∠BAD=2∠EAF，试探究线段BE、EF、FD之间的数量关系．
  小明同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG．再证明△AEF≌△AGF，可得出结论，他的结论应是

  ．
  （2）猜想论证．
  如图2，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E在线段BC上、F在线段CD延长线上．若∠BAD=2∠EAF，上述结论是否依然成立？若成立说明理由；若不成立，试写出相应的结论并给出你的证明．
  （3）拓展应用．
  如图3，在四边形ABCD中，∠BDC=45°，连接BC、AD，AB：AC：BC=3：4：5，AD=4，且∠ABD+∠CBD=180°．则△ACD的面积为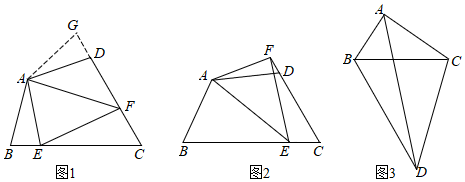

  ．
  
  组卷：1035引用：5难度：0.1

  解析

• 24．已知抛物线y=ax²+a（a＞0），G为抛物线的顶点．
  （1）如图1，抛物线经过点A（2，5）．
  ①求抛物线的解析式；
  ②若在第一象限抛物线上有点B，使S_△ABG=1，求点B的坐标；
  （2）将抛物线y=ax²+a绕顶点G旋转180°，新抛物线（如图2）交x轴C、D两点，点P为x轴上方抛物线上的一个动点，直线CP，DP分别交y轴于M、N两点，求OM•ON的最大值（用含a的式子表示）．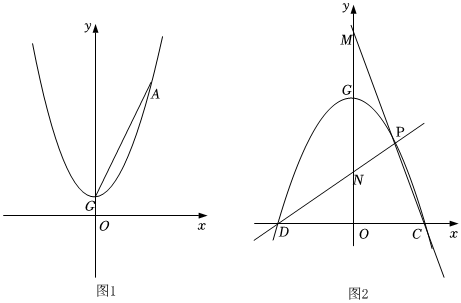
  
  组卷：528引用：3难度：0.3

  解析