2023-2024学年广东省佛山市顺德区容山中学高二（上）期中数学试卷

一．选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的

• 1．从甲，乙等五名同学中随机选3人参加社区服务工作，则甲，乙中至少有一人入选的概率为（　　）

  A． 3 10

  B． 9 10

  C． 2 5

  D． 3 5
  组卷：111引用：4难度：0.7

  解析

• 2．

  {

  a

  ，

  b

  ，

  c

  }

  为空间的一组基底，则下列各项中能构成基底的一组向量是（　　）

  A． a ， a + b ， a - b	B． b ， a + b ， a - b
  C． c ， a + b ， a - b	D． a + 2 b ， a + b ， a - b
  组卷：475引用：7难度：0.7

  解析

• 3．抛掷一枚质地均匀的骰子，设事件A：出现的点数为质数，事件B：出现的点数不小于3，则事件A与事件B（　　）

  A．相互独立	B．对立
  C．互斥但不对立	D．概率相等
  组卷：165引用：7难度：0.7

  解析

• 4．目前，国际上常用身体质量指数BMI=

  体重

  （

  单位

  ：

  kg

  ）

  身

  高

  2

  （

  单位

  ：

  m

  2

  ）

  来衡量人体胖瘦程度以及是否健康．某公司对员工的BMI值调查结果显示，男员工中，肥胖者的占比为

  3

  100

  ；女员工中，肥胖者的占比为

  2

  100

  ，已知公司男、女员工的人数比例为2：1，若从该公司中任选一名肥胖的员工，则该员工为男性的概率为（　　）

  A． 3 100

  B． 9 200

  C． 3 5

  D． 3 4
  组卷：166引用：7难度：0.7

  解析

• 5．过点A（2，3）且平行于直线2x+y-5=0的直线方程为（　　）

  A．x-2y+4=0

  B．2x+y-7=0

  C．x-2y+3=0

  D．x-2y+5=0
  组卷：311引用：3难度：0.7

  解析

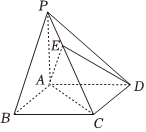• 6．我国古代数学名著《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图，四棱锥P-ABCD为阳马，PA⊥平面ABCD，且EC=2PE，若

  DE

  =

  x

  AB

  +

  y

  AC

  +

  z

  AP

  ，则x+y+z=（　　）

  A．1

  B．2

  C． 1 3

  D． 5 3
  组卷：1312引用：34难度：0.7

  解析

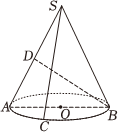• 7．如图，已知圆锥的底面半径为1，母线长为

  2

  ，AB为圆锥底面圆的直径，C是圆弧AB的中点，D是母线SA的中点，则异面直线SC与BD所成角的余弦值为（　　）

  A． 2 3

  B． 10 5

  C． 5 10

  D． 10 10
  组卷：64引用：2难度：0.6

  解析

四．解答题：本题共6小题，第17题10分，第18-22题每小题10分，共70分。解答应写出文字说明，证明过程或演算步骤。

• 21．已知直线l经过点P（-2，4）．
  （Ⅰ）若原点到直线l的距离为2，求直线l的方程；
  （Ⅱ）若直线l被两条相交直线l₁：2x-y-2=0和l₂：x+y-7=0所截得的线段恰被点P平分，求直线l的方程．
  组卷：493引用：4难度：0.6

  解析

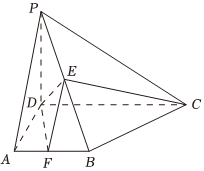• 22．如图，在四棱锥P-ABCD中，四边形ABCD是直角梯形，AD⊥AB，AB∥CD，PD=

  2

  AB，PB=CD=2AB=2AD，PC⊥DE，E是棱PB的中点．
  （1）证明：PD⊥平面ABCD；
  （2）若

  AF

  =

  λ

  AB

  （

  0

  ＜

  λ

  ≤

  1

  ）

  ，求平面DEF与平面PAB夹角的余弦值的最大值．
  组卷：566引用：5难度：0.3

  解析