2023-2024学年湖北省新高考联考协作体高一（上）联考数学试卷（10月份）

一、单项选择题（共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案填涂在答题卡相应位置上）

• 1．命题“∀x∈R，x²+2x+1＞0”的否定是（　　）

  A．∀x∈R，x2+2x+1≤0	B．∀x∈R，x2+2x+1＜0
  C．∃x∈R，使得x2+2x+1＜0	D．∃x∈R，使得x2+2x+1≤0
  组卷：139引用：14难度：0.8

  解析

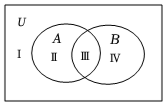• 2．设集合A，B均为U的子集，如图，A∩（∁_UB）表示区域（　　）

  A．Ⅰ

  B．Ⅱ

  C．Ⅲ

  D．Ⅳ
  组卷：190引用：8难度：0.7

  解析

• 3．下列集合关系中错误的是（　　）

  A．{（a,b）}⊆{a,b}

  B．{0，2}⊆Z

  C．∅⊆{0}

  D．{0，1}⊆{1，0}
  组卷：193引用：4难度：0.7

  解析

• 4．使x²＜4成立的一个充分不必要条件是（　　）

  A．x＜2

  B．0＜x＜2

  C．-2≤x≤2

  D．x＞0
  组卷：45引用：3难度：0.8

  解析

• 5．若“∃x∈R，ax²-3ax+9≤0”是假命题，则a的取值范围为（　　）

  A．[0，4]

  B．[0，4）

  C．（0，4）

  D．[4，+∞）
  组卷：121引用：6难度：0.8

  解析

• 6．已知不等式ax²+bx+1＞0的解集为

  {

  x

  |

  -

  1

  3

  ＜

  x

  ＜

  1

  2

  }

  ，则不等式x²-bx+a≥0的解集为（　　）

  A．{x|x≤-3或x≥-2}	B．{x|-3≤x≤-2}
  C．{x|-2≤x≤3}	D．{x|x≤-2或x≥3}
  组卷：143引用：6难度：0.7

  解析

• 7．已知函数f（x）=ax³+bx²，且-2＜f（1）＜3，-4＜f（-2）＜8，则f（-1）的取值范围为（　　）

  A．（-3， 7 3 ）

  B．（-3，4）

  C．（- 4 3 ，4）

  D．（- 4 3 ， 7 3 ）
  组卷：65引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）

• 21．为摆脱美国政府针对中国高科技企业的封锁，加强自主性，某企业计划加大对芯片研发部的投入，据了解，该企业研发部原有100名技术人员，年人均投入60万元，现将这100名技术人员分成两部分：技术人员和研发人员，其中技术人员x名（x∈N^*），调整后研发人员的年人均投入增加4x%，技术人员的年人均投入调整为

  60

  （

  m

  -

  2

  x

  25

  ）

  万元．
  （1）要使这（100-x）名研发人员的年总投入不低于调整前的100名技术人员的年总投入，求调整后的技术人员的人数x最多为多少人？
  （2）若技术人员在已知范围内调整后，必须研发人员的年总投入始终不低于技术人员的年总投入，求出正整数m的最大值．
  组卷：128引用：17难度：0.6

  解析

• 22．已知

  f

  （

  x

  ）

  =

  4

  x

  -

  a

  x

  2

  +

  b

  是定义在R上的奇函数，其中a,b∈R，且f（2）=1．
  （1）求a,b的值；
  （2）判断f（x）在[2，+∞）上的单调性，并用单调性的定义证明；
  （3）设g（x）=mx²-2x+2-m,若对任意的x₁∈[2，4]，总存在x₂∈[0，1]，使得f（x₁）=g（x₂）成立，求非负实数m的取值范围．
  组卷：73引用：8难度：0.5

  解析