当前位置：试卷中心 > 试卷详情

2022-2023学年四川省攀枝花市西区九年级（上）期中数学试卷

发布：2024/8/28 0:0:8

一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．下列根式是最简二次根式的是（　　）
A．
8
B．
27
C．
3
3
D．
1
2
组卷：459引用：6难度：0.7
解析
2．式子
2
-
x
在实数范围内有意义，则x的取值范围是（　　）
A．x≥-2 B．x≥2 C．x≤-2 D．x≤2
组卷：138引用：11难度：0.9
解析
3．下列方程是关于x的一元二次方程的是（　　）
A．ax²+bx+c=0 B．
1
x
2
+
1
x
=2
C．x²+2x=x²-1 D．3（x+1）²=2（x+1）
组卷：1719引用：150难度：0.9
解析
4．下列各组线段中，成比例线段的一组是（　　）
A．1，2，2，3 B．1，2，2，4 C．1，2，3，4 D．4，5，9，11
组卷：22引用：3难度：0.5
解析
5．下列各式计算正确的是（　　）
A．
8
3
-
2
3
=
6
B．
5
3
+
5
2
=
10
5
C．
4
3
×
2
2
=
8
6
D．
4
2
÷
2
2
=
2
2
组卷：1649引用：34难度：0.9
解析
6．已知
a
b
=
3
5
，则
a
a
+
b
的值为（　　）
A．
3
8
B．
8
5
C．
3
5
D．
8
3
组卷：1472引用：13难度：0.9
解析
7．已知2是关于x的方程：x²-x+a=0的一个解，则2a-1的值是（　　）
A．5 B．-5 C．3 D．-3
组卷：54引用：2难度：0.9
解析
8．用配方法解方程x²-2x-6=0时，原方程应变形为（　　）
A．（x+1）²=7 B．（x-1）²=7 C．（x+2）²=10 D．（x-2）²=10
组卷：92引用：4难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（解答应写出文字说明、证明过程或演算步骤．17题-22题每小题8分，23题每小题8分，24题12分，共70分）

23．阅读理解题，阅读材料，解决问题：
配方法是一种重要的数学方法，我们已经学习了用配方法解一元二次方程，并在此基础上得出了一元二次方程的求根公式．其实配方法还有很多重要的应用，例如我们可以用配方法求函数的最值以及取得最值的条件，见下面的例子：
例：求函数y=-x²-3x+2的最大值以及取得最大值的条件．
解：
y
=
-
x
2
-
3
x
+
2
=
-
（
x
2
+
3
x
+
9
4
-
9
4
）
+
2
=
-
（
x
+
3
2
）
2
+
17
4

∵
（
x
+
3
2
）
2
≥
0
，∴
-
（
x
+
3
2
）
2
≤
0
，∴
-
（
x
+
3
2
）
2
+
17
4
≤
17
4
，即
y
≤
17
4

∴y的最大值为
17
4
，此时
x
+
3
2
=
0
，
x
=
-
3
2
．
仿照上面的方法，请你解决下面的问题：
（1）已知函数y=-2x²-8x+1，当x=
时，函数有最大值为
；
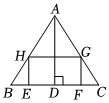
（2）如图，在△ABC中，BC=20，高AD=16，内接矩形EFGH的顶点E、F在BC上，G、H分别在AC、AB上，设HG=x,矩形EFGH的面积为y,求：
①y关于x的函数关系式；
②矩形EFGH的面积的最大值．
组卷：112引用：3难度：0.5
解析
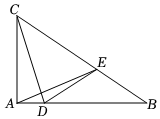24．如图，Rt△ABC的两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动，速度是1cm/秒，同时，点E沿BC从B向C运动，速度为2cm/秒．动点E到达点C时运动终止．连接DE、CD、AE．
（1）当动点运动几秒时，△BDE与△ABC相似？
（2）当动点运动几秒时，△BDE的面积为1.8cm²？
（3）在运动过程中是否存在某一时刻t,使CD⊥DE？若存在，直接写出t的值；若不存在，请说明理由．
组卷：83引用：6难度：0.4
解析