阅读理解题，阅读材料，解决问题：
配方法是一种重要的数学方法，我们已经学习了用配方法解一元二次方程，并在此基础上得出了一元二次方程的求根公式．其实配方法还有很多重要的应用，例如我们可以用配方法求函数的最值以及取得最值的条件，见下面的例子：
例：求函数y=-x2-3x+2的最大值以及取得最大值的条件．
解：y=-x2-3x+2=-（x2+3x+94-94）+2=-（x+32）2+174
∵（x+32）2≥0，∴-（x+32）2≤0，∴-（x+32）2+174≤174，即y≤174
∴y的最大值为174，此时x+32=0，x=-32．
仿照上面的方法，请你解决下面的问题：
（1）已知函数y=-2x2-8x+1，当x=-2-2时，函数有最大值为 99；
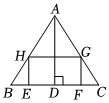
（2）如图，在△ABC中，BC=20，高AD=16，内接矩形EFGH的顶点E、F在BC上，G、H分别在AC、AB上，设HG=x,矩形EFGH的面积为y,求：
①y关于x的函数关系式；
②矩形EFGH的面积的最大值．
y
=
-
x
2
-
3
x
+
2
=
-
（
x
2
+
3
x
+
9
4
-
9
4
）
+
2
=
-
（
x
+
3
2
）
2
+
17
4
（
x
+
3
2
）
2
≥
0
-
（
x
+
3
2
）
2
≤
0
-
（
x
+
3
2
）
2
+
17
4
≤
17
4
y
≤
17
4
17
4
x
+
3
2
=
0
x
=
-
3
2
【答案】-2；9
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 0:0:8组卷：112引用：3难度：0.5
相似题
-
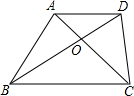1．如图，梯形ABCD中AD∥BC，对角线AC、BD交于0点，△AOD与△DOC的面积之比为3：7，则AD：BC=．发布：2025/1/28 8:0:2组卷：39引用：1难度：0.7 -
2．如图，在梯形ABCD中，AB∥CD，对角线AC、BD相交于点O，如果S△AOB=2S△AOD，AC=10，那么OC的长是．发布：2025/1/28 8:0:2组卷：107引用：1难度：0.4 -
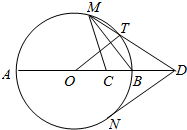3．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连接MC，MB，OT．
（Ⅰ）求证：DT•DM=DO•DC；
（Ⅱ）若∠DOT=60°，试求∠BMC的大小．发布：2025/1/28 8:0:2组卷：364引用：1难度：0.3
