2022-2023学年重庆市荣昌中学高二（上）第一次月考数学试卷

一、单选题

• 1．已知

  u

  =

  （

  1

  ，

  2

  ，

  1

  ）

  是直线l的方向向量，

  v

  =

  （

  2

  ，

  y

  ,

  2

  ）

  为平面α的法向量，若l⊥α，则y的值为（　　）

  A．-2

  B． - 1 2

  C． 1 4

  D．4
  组卷：266引用：4难度：0.8

  解析

• 2．某中学有高中生960人，初中生480人．为了了解学生的身体状况，用比例分配的分层随机抽样方法，从该校学生中抽取容量为n的样本，其中高中生有24人，那么n等于（　　）

  A．48

  B．36

  C．24

  D．12
  组卷：112引用：4难度：0.8

  解析

• 3．直线

  6

  x

  +

  2

  y

  -

  1

  =

  0

  的倾斜角为（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：805引用：7难度：0.7

  解析

• 4．为得到函数y=sin2x的图象，只需将函数y=cos（2x+

  π

  3

  ）的图象（　　）

  A．向右平移 5 π 12 个单位长度

  B．向左平移 5 π 12 个单位长度

  C．向左平移 5 π 6 个单位长度

  D．向右平移 5 π 6 个单位长度
  组卷：66引用：7难度：0.9

  解析

• 5．已知

  a

  =（2，-1，3），

  b

  =（-1，4，-2），

  c

  =（1，3，λ），若

  a

  ，

  b

  ，

  c

  三向量共面，则实数λ等于（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：451引用：72难度：0.7

  解析

• 6．已知正三棱柱ABC-A₁B₁C₁中，AB=2，AA₁=1，点D为AB中点，则异面直线BC与C₁D所成角的余弦值为（　　）

  A． 3 4

  B． 3 2

  C． 2 3

  D． 1 2
  组卷：152引用：4难度：0.6

  解析

• 7．已知a＞0，b＞0，两直线l₁：（a-1）x+y-1=0，l₂：x+2by+1=0且l₁⊥l₂，则

  2

  a

  +

  1

  b

  的最小值为（　　）

  A．2

  B．4

  C．8

  D．9
  组卷：2592引用：40难度：0.7

  解析

四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．在△ABC中，角A，B，C的对边分别为a,b,c,且a-bcosC=

  3

  csinB．
  （1）求B；
  （2）若a=2，且△ABC为锐角三角形，求△ABC的面积S的取值范围．
  组卷：841引用：4难度：0.4

  解析

• 22．如图，四边形ABCD为梯形，AB∥CD，∠C=60°，CD=2CB=4AB=4，点E在线段CD上，且BE⊥CD．现将△ADE沿AE翻折到△PAE的位置，使得PC=

  10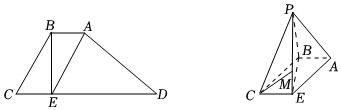

  ．
  
  （1）证明：AE⊥PB；
  （2）点M是线段PE上的一点（不包含端点），是否存在点M，使得二面角P-BC-M的余弦值为

  6

  3

  ？若存在，则求出

  ME

  PE

  ；若不存在，请说明理由．
  组卷：244引用：7难度：0.6

  解析