2023-2024学年安徽省宿州市埇桥区宿城一中九年级（上）第一次月考数学试卷

一、选择题（共10小题，每题4分，共40分）

• 1．若关于x的方程（m-2）

  x

  m

  2

  -

  2

  +x=0是一元二次方程，则m的值是（　　）

  A．-2

  B．±2

  C．3

  D．±3
  组卷：238引用：13难度：0.7

  解析

• 2．有下列命题：
  ①对角线相等且互相平分的四边形是矩形；
  ②对角线互相垂直的四边形是菱形；
  ③对角线垂直且相等的四边形是正方形；
  ④四边相等的四边形是菱形．
  其中，真命题有（　　）个．

  A．1

  B．2

  C．3

  D．4
  组卷：17引用：1难度：0.6

  解析

• 3．已知关于x的方程（k-3）x²-4x+2=0有实数根，则k的取值范围是（　　）

  A．k≤5

  B．k＜5且k≠3

  C．k≤5且k≠3

  D．k≥5
  组卷：1593引用：13难度：0.6

  解析

• 4．用配方法解方程3x²+4x+1=0时，可以将方程化为（　　）

  A． （ x + 2 3 ） 2 = 1 9	B．（x+2）2=3
  C． （ x + 2 3 ） 2 = 1 3	D． （ 3 x + 2 3 ） 2 = 1 9
  组卷：71引用：2难度：0.6

  解析

• 5．根据表格中的信息，估计一元二次方程ax²+bx+c=0（a、b、c为常数，a≠0）的一个解x的范围为（　　）
  

  x	0.4	0.5	0.6	0.7	0.8
  ax2+bx+c	-0.44	-0.25	-0.04	0.19	0.44

  A．0.4＜x＜0.5

  B．0.5＜x＜0.6

  C．0.6＜x＜0.7

  D．0.7＜x＜0.8
  组卷：119引用：6难度：0.5

  解析

• 6．若顺次连接四边形ABCD各边的中点所得的四边形是菱形，则四边形ABCD的两条对角线AC，BD一定是（　　）

  A．互相平分	B．互相平分且相等
  C．互相垂直	D．相等
  组卷：174引用：4难度：0.5

  解析

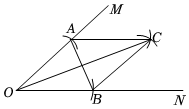• 7．如图，在∠MON的两边上分别截取OA，OB，使OA=OB；再分别以点A，B为圆心，OA长为半径作弧，两弧交于点C；再连接AC，BC，AB，OC．若AB=10，OA=13．则四边形AOCB的面积是（　　）

  A．65

  B．120

  C．130

  D．240
  组卷：96引用：5难度：0.5

  解析

三、解答题（本大题共9题，共90分）

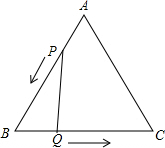• 22．已知：如图，△ABC是边长6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是2cm/s,当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），解答下列问题：
  （1）当t为何值时，△PBQ是直角三角形；
  （2）是否存在某一时刻t,使四边形APQC的面积是△ABC面积的四分之三？如果存在，求出相应的t值；不存在，说明理由．
  组卷：254引用：1难度：0.6

  解析

• 23．如图，在四边形ABCD中，点E是直线BC上一点，将射线AE绕点A逆时针旋转α度交直线CD于点F．
  （1）如图①，若四边形ABCD为菱形，点E在线段BC上．∠B=60°，α=60°，求证：AE=AF；
  （2）如图②，若四边形ABCD为正方形，点E在线段BC的延长线上，α=45°，连接EF，试猜想线段BE，DF与EF之间的数量关系，并加以证明；
  （3）若四边形ABCD为正方形，α=45°，AB=4，

  BE

  =

  1

  2

  BC

  ，连接EF，请直接写出EF的长．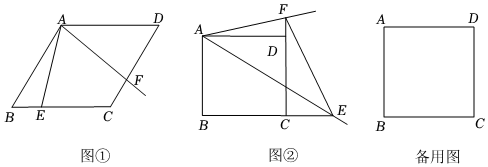
  组卷：235引用：1难度：0.1

  解析