2022-2023学年福建省南平市浦城县高二（上）期中数学试卷

一、单选题（本大题共8小题，每小题5分，总40分.每小题只有一个选项符合题意）

• 1．直线3x+4y+12=0与圆（x-1）²+（y+1）²=9的位置关系是（　　）

  A．相交且过圆心	B．相切
  C．相离	D．相交但不过圆心
  组卷：886引用：17难度：0.9

  解析

• 2．抛物线

  y

  =

  4

  3

  x

  2

  的焦点坐标为（　　）

  A． （ 0 ， 1 3 ）

  B． （ 1 3 ， 0 ）

  C． （ 0 ， 3 16 ）

  D． （ 3 16 ， 0 ）
  组卷：206引用：5难度：0.8

  解析

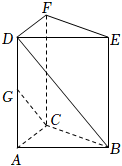• 3．三棱柱ABC-DEF中，G为棱AD的中点，若

  BA

  =

  a

  ，

  BC

  =

  b

  ，

  BD

  =

  c

  ，则

  CG

  =（　　）

  A． - a + b - c

  B． 1 2 a - b + 1 2 c

  C． - 1 2 a + b + c

  D． - 1 2 a + 1 2 b + c
  组卷：1424引用：31难度：0.7

  解析

• 4．已知圆（x+1）²+（y+2）²=4关于直线ax+by+1=0（a＞0，b＞0）对称，则

  1

  a

  +

  2

  b

  的最小值为（　　）

  A． 5 2

  B．9

  C．4

  D．8
  组卷：838引用：12难度：0.8

  解析

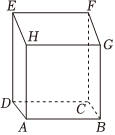• 5．在如图所示的六面体中，四边形ADEH和BCFG均为直角梯形，A，D，C，B为直角顶点，其他四个面均为矩形，AB=BG=3，FC=4，BC=1，则平面EFGH与平面ABCD所成的角为（　　）

  A．30°

  B．45°

  C．135°

  D．45°或135°
  组卷：8引用：3难度：0.5

  解析

• 6．已知O为坐标原点，焦点在x轴上的曲线C：

  x

  2

  3

  +

  y

  2

  m

  2

  =

  1

  的离心率e满足6e²-5e+1≤0，A，B是x轴与曲线C的交点，P是曲线C上异于A，B的一点，延长PO交曲线C于另一点Q，则tan∠OBP•tan∠OBQ的取值范围是（　　）

  A． [ 3 4 ， 8 9 ]

  B． [ 3 2 ， 5 2 ]

  C． [ 1 4 ， 5 9 ]

  D． [ 1 4 ， 2 ]
  组卷：13引用：2难度：0.6

  解析

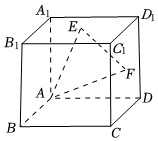• 7．已知正方体ABCD-A₁B₁C₁D₁的棱长为2，E，F分别为上底面A₁B₁C₁D₁和侧面CDD₁C₁的中心，则点C到平面AEF的距离为（　　）

  A． 4 11 11

  B． 11 4

  C． 11 11

  D． 2 11 11
  组卷：144引用：4难度：0.7

  解析

四、简答题（本大题共6小题，第17小题10分，第18-22小题每题12分，共70分.解答过程必修有必要的文字说明，公式和解题过程.）

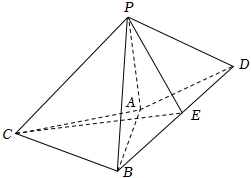• 21．如图，在六面体PABCD中，△PAB是等边三角形，二面角P-AB-D的平面角为30°，PC=AB=

  2

  AD

  =

  2

  BD

  =

  2

  AC

  =

  2

  BC=4．
  （1）证明：AB⊥PD；
  （2）若点E为线段BD上一动点，求直线CE与平面PAB所成角的正切的最大值．
  组卷：227引用：4难度：0.6

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  2

  2

  ，且过点（0，1）．
  （1）求椭圆C的标准方程；
  （2）过点P（2，0）且不垂直于x轴的直线l与椭圆C相交于A、B两点，若B点关于x轴的对称点为E，证明：直线AE与x轴相交于定点．
  组卷：10引用：1难度：0.5

  解析