2019-2020学年山西省晋中市灵石县八年级（下）期末数学试卷

一、选择题（每小题3分，共30分）

• 1．将多项式a²b-b³分解因式的结果是（　　）

  A．b（a2-b2）	B．b（a-b）2
  C．（ab+b）（a-b）	D．b（a+b）（a-b）
  组卷：48引用：3难度：0.7

  解析

• 2．如图，已知在▱ABCD中，对角线AC，BD相交于点O，若AB=7，AC=8，BD=10，则△OCD的周长为（　　）

  A．12

  B．13

  C．15

  D．16
  组卷：20引用：1难度：0.8

  解析

• 3．下列车标，可看作图案的某一部分经过平移所形成的是（　　）

  A．

  B．

  C．

  D．
  组卷：166引用：3难度：0.9

  解析

• 4．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
  
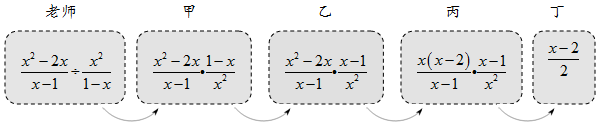
  接力中，自己负责的一步出现错误的是（　　）

  A．只有乙

  B．甲和丁

  C．乙和丙

  D．乙和丁
  组卷：4898引用：60难度：0.7

  解析

• 5．在直角三角形ABC中，已知∠C=90°，∠A=60°，AC=10

  3

  ，则BC等于（　　）

  A．30

  B．10

  C．20

  D．5 3
  组卷：124引用：2难度：0.7

  解析

• 6．如图，以△ABD的顶点B为圆心，以BD为半径作弧交边AD于点E，分别以点D、点E为圆心，BD长为半径作弧，两弧相交于不同于点B的另一点F，再过点B和点F作直线BF．则作出的直线是（　　）

  A．线段AD的垂线但不一定平分线段AD

  B．线段AD的垂直平分线

  C．∠ABD的平分线

  D．△ABD的中线
  组卷：755引用：7难度：0.6

  解析

• 7．小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC、BD的中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（　　）

  A．对角线互相平分的四边形是平行四边形

  B．两组对角分别相等的四边形是平行四边形

  C．两组对边分别相等的四边形是平行四边形

  D．两组对边分别平行的四边形是平行四边形
  组卷：1667引用：24难度：0.8

  解析

三、解答题（共75分）

• 22．综合与实践
  问题情境：在综合与实践课上，老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合，并让一个三角板固定，另一个绕直角顶点旋转”为主题开展数学活动，如图1，三角板ABC和三角板CDE都是等腰直角三角形，∠C=90°，点D，E分别在边BC，AC上，连接AD，点M，P，N分别为DE，AD，AB的中点．试判断线段PM与PN的数量关系和位置关系．
  探究展示：勤奋小组发现，PM=PN，PM⊥PN．并展示了如下的证明方法：
  ∵点P，N分别是AD，AB的中点，∴PN∥BD，

  PN

  =

  1

  2

  BD

  ．
  ∵点P，M分别是AD，DE的中点，∴PM∥AE，

  PM

  =

  1

  2

  AE

  ．（依据1）
  ∵CA=CB，CD=CE，∴BD=AE，∴PM=PN．
  ∵PN∥BD，∴∠DPN=∠ADC．
  ∵PM∥AE，∴∠DPM=∠DAC．
  ∵∠BCA=90°，∴∠ADC+∠CAD=90°．（依据2）
  ∴∠MPN=∠DPM+∠DPN=∠CAD+∠ADC=90°．∴PM⊥PN．
  反思交流：
  （1）①上述证明过程中的“依据1”，“依据2”分别是指什么？
  ②试判断图1中，MN与AB的位置关系，请直接回答，不必证明；
  （2）创新小组受到勤奋小组的启发，继续进行探究，把△CDE绕点C逆时针方向旋转到如图2的位置，发现△PMN是等腰直角三角形，请你给出证明；
  （3）缜密小组的同学继续探究，把△CDE绕点C在平面内自由旋转，当CD=4，CB=10时，求△PMN面积的最大值．
  
  组卷：662引用：3难度：0.1

  解析

• 23．如图1，OA=2，OB=4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC
  
  （1）求C点的坐标．
  （2）如图2，在平面内是否存在一点H，使得以A、C、B、H为顶点的四边形为平行四边形？若存在，请写出H点坐标；若不存在，请说明理由．
  组卷：700引用：3难度：0.5

  解析