综合与实践
问题情境：在综合与实践课上，老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合，并让一个三角板固定，另一个绕直角顶点旋转”为主题开展数学活动，如图1，三角板ABC和三角板CDE都是等腰直角三角形，∠C=90°，点D，E分别在边BC，AC上，连接AD，点M，P，N分别为DE，AD，AB的中点．试判断线段PM与PN的数量关系和位置关系．
探究展示：勤奋小组发现，PM=PN，PM⊥PN．并展示了如下的证明方法：
∵点P，N分别是AD，AB的中点，∴PN∥BD，PN=12BD．
∵点P，M分别是AD，DE的中点，∴PM∥AE，PM=12AE．（依据1）
∵CA=CB，CD=CE，∴BD=AE，∴PM=PN．
∵PN∥BD，∴∠DPN=∠ADC．
∵PM∥AE，∴∠DPM=∠DAC．
∵∠BCA=90°，∴∠ADC+∠CAD=90°．（依据2）
∴∠MPN=∠DPM+∠DPN=∠CAD+∠ADC=90°．∴PM⊥PN．
反思交流：
（1）①上述证明过程中的“依据1”，“依据2”分别是指什么？
②试判断图1中，MN与AB的位置关系，请直接回答，不必证明；
（2）创新小组受到勤奋小组的启发，继续进行探究，把△CDE绕点C逆时针方向旋转到如图2的位置，发现△PMN是等腰直角三角形，请你给出证明；
（3）缜密小组的同学继续探究，把△CDE绕点C在平面内自由旋转，当CD=4，CB=10时，求△PMN面积的最大值．
PN
=
1
2
BD
PM
=
1
2
AE
【考点】几何变换综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/1 8:0:9组卷：662引用：3难度：0.1
相似题
-
1．如图①，在Rt△ABC中，∠B=90°，AB=5，BC=12，CD=5，DE∥AB．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）①当α=0°时，=；②当α=180°时，AEBD=．AEBD
（2）试判断：当0≤α≤360°时，的大小有无变化？请仅就图②的情形给出证明．AEBD
（3）当△EDC旋转到A，D，E三点共线时，直接写出线段BD的长．
发布：2025/5/23 20:0:1组卷：194引用：3难度：0.3 -
2．如图，在平面直角坐标系中有Rt△ABO，∠BAO=90°，∠ABO=30°，B（-8，0）．将三角形ABO绕着点O顺时针方向旋转，旋转后点A与A1，点B与B1相重合．
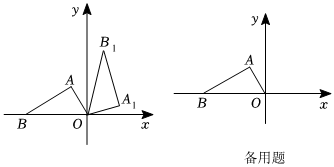
（1）当旋转角为60°时，求点B1的坐标；
（2）当点B1落在BA的延长线上时，求点B1的坐标．
（3）若点E为AB的中点，求EB1的最大值和最小值．（直接写出结果即可）发布：2025/5/23 18:0:1组卷：688引用：5难度：0.1 -
3．如图1，在△ABC中，∠BAC=90°，AB=AC=4，点E为边AC上一点，以AE为斜边，在△ABC外，作△ADE，使得∠ADE=90°，且DE=DA．现将△ADE绕点A逆时针旋转，旋转角为α（0°＜α＜90°），连接BE．
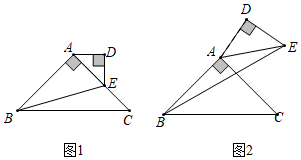
（1）如图2，当α=15°且BE∥AD时，求BE的长；
（2）连接CE，设CE的中点为点F，AE的中点为点H，连接DF，直线DF与线段BE交于点G，连接GH．
①求证：DF⊥BE；
②探索线段GH，GD，GE之间的数量关系．发布：2025/5/23 22:0:2组卷：430引用：2难度：0.2
