2022-2023学年浙江省金华一中高二（下）月考数学试卷（6月份）

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若集合A={x∈Z|3x-x²＞0}，则满足A∪B={1，2，3，4}的集合B的个数为（　　）

  A．2

  B．3

  C．4

  D．16
  组卷：170引用：4难度：0.8

  解析

• 2．已知实数a,b满足lga+lgb=lg（a+2b），则2a+b的最小值是（　　）

  A．5

  B．9

  C．13

  D．18
  组卷：424引用：3难度：0.7

  解析

• 3．若（1-2x）²⁰²³=a₀+a₁x+a₂x²+…+a₂₀₂₃x²⁰²³，则

  a

  1

  2

  +

  a

  2

  2

  2

  +

  …

  +

  a

  2023

  2

  2023

  的值为（　　）

  A．-1

  B．0

  C． 1 2

  D．1
  组卷：217引用：3难度：0.7

  解析

• 4．“sin2α＞0”是“tanα＞0”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：118引用：4难度：0.8

  解析

• 5．已知函数

  f

  （

  x

  ）

  =

  （ x + 1 ） 2 ，	x ≤ 0 ，
  | lgx | ，	x ＞ 0 ，

  若函数g（x）=f（x）-b有四个不同的零点，则实数b的取值范围为（　　）

  A．（0，1]

  B．[0，1]

  C．（0，1）

  D．（1，+∞）
  组卷：498引用：9难度：0.6

  解析

• 6．“总把新桃换旧符”（王安石）、“灯前小草写桃符”（陆游），春节是中华民族的传统节日，在宋代人们用写“桃符”的方式来祈福避祸，而现代人们通过贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿，某商家在春节前开展商品促销活动，顾客凡购物金额满80元，则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件，若有5名顾客都领取一件礼品，则他们中恰有3人领取的礼品种类相同的概率是（　　）

  A． 140 243

  B． 40 243

  C． 20 81

  D． 40 81
  组卷：149引用：3难度：0.8

  解析

• 7．已知a=sin1，

  b

  =

  3

  π

  ，

  c

  =

  1

  lo

  g

  3

  π

  ，则a,b,c的大小关系为（　　）

  A．a＞c＞b

  B．c＞b＞a

  C．c＞a＞b

  D．b＞a＞c
  组卷：92引用：3难度：0.6

  解析

四、解答题：本题共6小题，70分.解答应写出文字说明、证明过程或演算步骤.

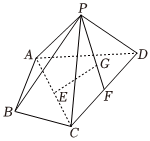• 21．如图，在四棱锥P-ABCD中，AB=BC=

  21

  2

  ，AD=CD=AC=2

  3

  ，E，F分别为AC，CD的中点，点G在PF上，且G为三角形PCD的重心．
  （1）证明：GE∥平面PBC；
  （2）若PA=PC，PA⊥CD，四棱锥P-ABCD的体积为3

  3

  ，求直线GE与平面PCD所成角的正弦值．
  组卷：222引用：2难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  ax

  +

  lnx

  -

  x

  ．
  （1）若a=1，求f（x）的极值；
  （2）若f（x）有三个极值点x₁，x₂，x₃，x₁＜x₂＜x₃，且

  x

  1

  x

  3

  ≤

  2

  ln

  2

  ，求a的最小值．
  组卷：119引用：3难度：0.3

  解析