当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省黄石八中八年级（上）期中数学试卷

发布：2024/9/5 15:0:8

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1．下列图案中，是轴对称图形的是（　　）
A． B． C． D．
组卷：289引用：11难度：0.8
解析
2．已知线段a=6cm,b=8cm,则下列线段中，能与a,b组成三角形的是（　　）
A．2cm B．10cm C．14cm D．16cm
组卷：131引用：7难度：0.7
解析
3．下列图形不具有稳定性的是（　　）
A． B． C． D．
组卷：120引用：6难度：0.7
解析
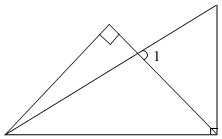4．将一副三角板按如图方式重叠，则∠1的度数为（　　）
A．45° B．60° C．75° D．85°
组卷：332引用：8难度：0.7
解析
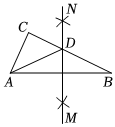5．如图，在△ABC中，分别以点A和点B为圆心，大于
1
2
AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB=8，则△ABC的周长为（　　）
A．8 B．10 C．18 D．20
组卷：927引用：15难度：0.5
解析
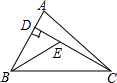6．如图，在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，若BC=16，DE=6，则△BCE的面积等于（　　）
A．36 B．48 C．60 D．72
组卷：196引用：2难度：0.7
解析
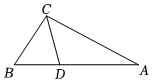7．如图，△ABC中，∠B=2∠A，∠ACB的平分线CD交AB于点D，已知AC=16，BC=9，则BD的长为（　　）
A．6 B．7 C．8 D．9
组卷：664引用：3难度：0.4
解析
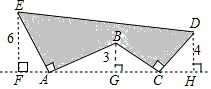8．如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（　　）
A．50 B．62 C．65 D．68
组卷：13403引用：131难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共7小题，共62分。解答应写出必要的文字说明、证明过程或演算步骤）

24．问题背景：
如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是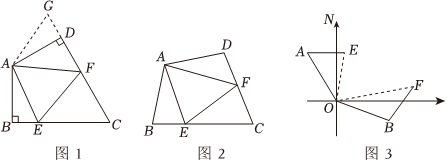
；

探索延伸：
如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠EAF=
1
2
∠BAD，上述结论是否仍然成立，并说明理由；
实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．
组卷：2471引用：115难度：0.3
解析
25．对于平面直角坐标系xOy中的线段MN及点Q，给出如下定义：
若点Q满足QM=QN，则称点Q为线段MN的“中垂点”；当QM=QN=MN时，称点Q为线段MN的“完美中垂点”．
（1）如图1，A（4，0），下列各点中，线段OA的中垂点是
．
Q₁（0，4），Q₂，（2，-4），Q₃（1，
3
）
（2）如图2，点A为x轴上一点，若Q（2，2
3
）为线段OA的“完美中垂点”，写出线段OQ的两个“完美中垂点”是
和
，两者的距离是
．
（3）如图3，若点A为x轴正半轴上一点，点Q为线段OA的“完美中垂点”，点P（0，m）在y轴上，在线段PA上方画出线段AP的“完美中垂点”M，直接写出MQ=
（用含m的式子表示）．并求出∠MQA（写出简单思路即可）．
组卷：2846引用：9难度：0.3
解析