2023-2024学年山东省枣庄市峄城区吴林中学九年级（上）第一次月考数学试卷

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是正确的．

• 1．下列哪个方程是一元二次方程（　　）

  A．x+2y=1

  B．x2-2x+3=0

  C．x2- 1 x =3

  D．ax2+bx+c=0
  组卷：160引用：6难度：0.9

  解析

• 2．顺次连接四边形ABCD四边的中点所得的四边形为矩形，则四边形ABCD一定满足（　　）

  A．AC⊥BD

  B．AB=BC

  C．AC=BD

  D．AB⊥BC
  组卷：169引用：3难度：0.7

  解析

• 3．根据下列表格中的对应值：

  x	3.23	3.24	3.25	3.26
  y=ax2+bx+c	-0.06	-0.02	0.03	0.09

  判断方程ax²+bx+c=0（a≠0，a、b、c为常数）的一个解x的范围是（　　）

  A．3＜x＜3.23	B．3.23＜x＜3.24
  C．3.24＜x＜3.25	D．3.25＜x＜3.26
  组卷：432引用：20难度：0.6

  解析

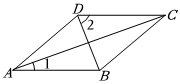• 4．如图，菱形ABCD中，连接AC，BD，若∠1=20°，则∠2的度数为（　　）

  A．20°

  B．60°

  C．70°

  D．80°
  组卷：2012引用：21难度：0.7

  解析

• 5．用配方法解方程x²-4x-1=0时，配方后正确的是（　　）

  A．（x+2）2=3

  B．（x+2）2=17

  C．（x-2）2=5

  D．（x-2）2=17
  组卷：2999引用：56难度：0.6

  解析

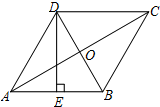• 6．如图，菱形ABCD的对角线AC、BD相交于点O，DE⊥AB于点E，若AB=5，DE=4，则在下列结论中正确的是（　　）

  A．DB=5

  B．AE=4

  C．BE=2

  D．OA=3 2
  组卷：508引用：6难度：0.8

  解析

• 7．据国家统计局发布的《2022年国民经济和社会发展统计公报》显示，2020年和2022年全国居民人均可支配收入分别为3.2万元和3.7万元．设2020年至2022年全国居民人均可支配收入的年平均增长率为x,依题意可列方程为（　　）

  A．3.2（1-x）2=3.7	B．3.2（1+x）2=3.7
  C．3.7（1-x）2=3.2	D．3.7（1+x）2=3.2
  组卷：2297引用：51难度：0.6

  解析

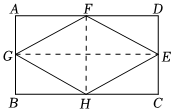• 8．如图，将矩形纸片ABCD对折，使边AB与DC，BC与AD分别重合，展开后得到四边形EFGH．若AB=2，BC=4，则四边形EFGH的面积为（　　）

  A．2

  B．4

  C．5

  D．6
  组卷：553引用：14难度：0.7

  解析

三、解答题：本大题共8小题，共72分，解答时，要写出必要的文字说明，证明过程或演算步骤．

• 23．正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°．将△DAE绕点D逆时针旋转90°，得到△DCM．
  （1）求证：EF=FM；
  （2）当AE=1时，求EF的长．
  组卷：2571引用：66难度：0.1

  解析

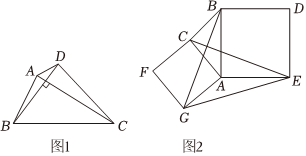• 24．小明学习了平行四边形这一章后，对特殊四边形的探究产生了兴趣，发现另外一类特殊四边形，如图1，我们把两条对角线互相垂直的四边形叫做垂美四边形．
  （1）概念理解：在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是

  
  （2）性质探究：通过探究，直接写出垂美四边形ABCD的面积S与两对角线AC，BD之间的数量关系：

  ．
  （3）问题解决：如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CG，BE，GE，已知AC=4，AB=5．
  ①求证：四边形BCGE为垂美四边形；
  ②求出四边形BCGE的面积．
  组卷：552引用：6难度：0.3

  解析