当前位置：试卷中心 > 试卷详情

2021-2022学年浙江省宁波市慈溪市校级七年级（下）期末数学试卷

发布：2024/6/5 8:0:7

一、选择题（每小题3分，共30分）

1．下列生活中的现象，属于平移的是（　　）
A．电梯上升
B．汽车雨刮器的运动
C．运动场国旗的飘动
D．投影片的文字经投影显示到屏幕
组卷：16引用：1难度：0.8
解析
2．下面各调查中，适合抽样调查的是（　　）
A．对全班同学的身高情况的调查
B．登机前对旅客的安全检查
C．对宁波市居民去年阅读量的调查
D．学校组织学生进行核酸检测
组卷：6引用：1难度：0.7
解析
3．下列计算正确的是（　　）
A．a³•a²=a⁶ B．a⁵+a⁵=a¹⁰
C．（-3a³）²=6a⁶ D．（a³）²•a=a⁷
组卷：39引用：4难度：0.8
解析
4．已知某新冠疫苗载体腺病毒的直径为0.000075毫米，将0.000075毫米用科学记数法可表示为（　　）
A．7.5×10^-5 毫米 B．0.75×10^-5 毫米
C．7.5×10^-4 毫米 D．75×10^-5 毫米
组卷：10引用：1难度：0.7
解析
5．
x
=
2
y
=
-
1
是某个二元一次方程组的解，则这个方程组可能是（　　）
A．
x
+
3
y
=
5
x
+
y
=
1
B．
x
=
y
+
3
y
+
2
x
=
5
C．
x
=
-
2
y
x
=
3
y
+
1
D．
2
x
-
y
=
5
x
+
y
=
1
组卷：29引用：1难度：0.7
解析
6．若x²+2（m-3）x+4是关于x的完全平方式，则m的值（　　）
A．±4 B．5 C．1 D．5或1
组卷：95引用：5难度：0.6
解析
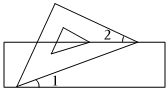7．把一块含有45°角的三角板与直尺如图放置．如果∠1=20°，那么∠2的度数是（　　）
A．15° B．20° C．25° D．30°
组卷：17引用：1难度：0.6
解析
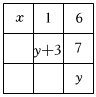8．九宫格是一种古老的数学游戏，它要求在3×3的矩阵中，填入1-9这9个数字，并且横向、纵向、斜向上的3个数字之和皆相等．图中九宫格中字母x所代表的数是（　　）
A．5 B．8 C．9 D．4
组卷：54引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（第17、18题各6分，第19题7分，第20、21题各8分，第22题

23．若一个整数能表示成a²+b²（a,b是正整数）的形式，则称这个数为“完美数”．
例如：∵13=2²+3²，∴13是“完美数”；
再如：∵a²+2ab+2b²=（a+b）²+b²（ a,b是正整数），
∴a²+2ab+2b² 也是“完美数”．
（1）请你写出一个大于30小于40的“完美数”，并判断117是否为“完美数”，请说明理由．
（2）若4m²+12mn+an²（m,n,a都是正整数）是“完美数”，写出两个a的可能的值．
（3）试判断（a²+b²）（4a²+c²）（ a,b,c是正整数）是否为“完美数”，并说明理由．
组卷：116引用：1难度：0.6
解析
24．我市某包装生产企业承接了一批无盖礼品盒制作业务，为了确保质量，该企业进行试生产．他们购得规格长170cm的标准板材作为原材料，每张标准板材可按照裁法一裁得2张A型、1张B型板材还多出10cm.也可以按照裁法二裁得1张A型、2张B型板材还多出30cm（如图，多出的10cm,30cm不能拼接使用）．

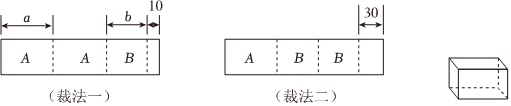
（1）列出方程（组），求出图中A型和B型板材的长度a与b的值．
（2）若将m张标准板材用裁法一裁剪，n张标准板材用裁法二裁剪，两种裁法共生产A型板材和B型板材各几张？（用含m,n的代数式表示）
（3）将得到的A，B两种板材作为侧面和底面，做成无盖礼品盒（如图所示，每个礼盒用3个A型板材和2个B型板材）．
①现有长为170cm的标准板材50张，能否恰好用完所裁得的A，B两种板材，制成无盖礼品盒．若能，求出礼品盒的只数；若不能，请问最多能制成几只礼品盒？
②来购时，170cm的标准板材的张数可在81张至96张之间选择，为使所裁得的A，B两种板材恰好全部用完，采购员可采购几张170cm的标准板材？做成的无盖礼品盒可以是多少个？请说明理由．
组卷：156引用：1难度：0.5
解析