2021-2022学年浙江省宁波市余姚市七年级(下)期末数学试卷
发布:2024/6/9 8:0:9
一、选择题(每小题3分,共30分)
-
1.如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成内错角的是( )
组卷:56引用:1难度:0.8 -
2.下面调查中,适合全面调查的是( )
组卷:25引用:1难度:0.5 -
3.红细胞的平均直径是0.0000072m,0.0000072这个数用科学记数法可表示为( )
组卷:129引用:6难度:0.8 -
4.“潮涌”是2022年杭州亚运会会徽,钱塘江和钱江潮头是会徽的形象核心,如图(1)是会徽的一部分,图(1)通过四次变换使它组合成一个新图案如图(2).在这四次变换中,是由该图经过平移得到的是( )
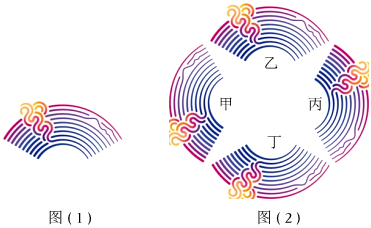 组卷:22引用:3难度:0.5
组卷:22引用:3难度:0.5 -
5.下列运算正确的是( )
组卷:689引用:7难度:0.7 -
6.将
中的a,b都扩大3倍,则分式的值( )aba+b组卷:55引用:1难度:0.7 -
7.下列从左到右的变形中,是因式分解的是( )
组卷:398引用:6难度:0.7 -
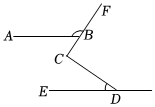 8.如图,AB∥DE,BC⊥CD,设∠ABF=α,∠CDE=β,则α与β之间的数量关系正确的是( )组卷:217引用:3难度:0.5
8.如图,AB∥DE,BC⊥CD,设∠ABF=α,∠CDE=β,则α与β之间的数量关系正确的是( )组卷:217引用:3难度:0.5
三、解答题(第17、18题各6分,第19~22题各8分,第23题10分,第24题12分,共66分)
-
23.杨梅是我市特产水果之一,素有“初疑一颗值千金”之美誉!某杨梅园的杨梅除了直接销售到市区外,还可以让市民去园区采摘.已知杨梅在市区和园区的销售价格分别是15元/千克和10元/千克,该杨梅园今年六月第一周一共销售了1000千克,销售收入12000元.
(1)该杨梅园今年六月第一周市区和园区分别销售了多少千克杨梅?
(2)为了促销,该杨梅园决定六月第二周将市区和园区销售价格均以相同折扣进行销售,小方发现用3240元购买市区的重量比用2430元购买园区的重量少30千克,求本次活动对市区和园区进行几折销售?
(3)在(2)的促销条件下,杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等.若第二周杨梅在市区的销量为a千克,园区的销量为b千克,请直接写出a与b的数量关系.组卷:310引用:3难度:0.6 -
24.【学习材料】十字相乘法
对于形如ax2+bxy+cy2的关于x、y二次三项式进行因式分解时,把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
例:分解因式:x2-2xy-8y2.
解:如图1,其中1=1×1,-8=(-4)×2,而-2=1×(-4)+1×2,∴x2-2xy-8y2=(x-4y)(x+2y).
而对于形如ax2+bxy+cy2+dx+ey+f的关于x、y的二元二次式也可以用两次十字相乘法来分解.如图2,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d;即第1、2列、第2、3列和第1、3列都满足十字相乘规则:则原式=(mx+py+j)(nx+qy+k).
例:分解因式:x2+2xy-3y2+3x+y+2.
解:如图3,其中1=1×1,-3=(-1)×3,2=1×2,而2=1×3+1×(-1),1=(-1)×2+3×1,3=1×2+1×1,
∴x2+2xy-3y2+3x+y+2=(x-y+1)(x+3y+2).
【知识应用】请根据以上材料中的方法,解决下列问题:
(1)通过十字相乘法分解因式得ax2+bx-7=(x-1)(2x+7),则a=,b=.
(2)分解因式:x2-7xy+6y2=;
6x2-5xy-6y2+2x+23y-20=;
(3)若x2+xy-2y2=0且2x+y≠1,求代数式的值.2x2+3xy+y2-x-y2x2-xy-y2-x+y组卷:597引用:2难度:0.5


