2022-2023学年吉林省长春市绿园区新解放学校高二（下）期中数学试卷

一、单项选择题（本题共8小题，每小题5分，共40分.）

• 1．

  （

  sin

  π

  3

  ）

  ′

  =（　　）

  A． cos π 3

  B． - 1 2

  C．0

  D． 3 2
  组卷：77引用：4难度：0.8

  解析

• 2．两个变量y与x的回归模型中，分别选择了4个不同的模型，它们的相关系数r如表，其中拟合效果最好的模型是（　　）
  

  模型	模型1	模型2	模型3	模型4
  相关系数r	0.48	0.96	0.15	0.30

  A．模型1

  B．模型2

  C．模型3

  D．模型4
  组卷：103引用：2难度：0.8

  解析

• 3．设ξ是一个离散型随机变量，其分布列为如表，则q=（　　）
  

  ξ	-1	0	1
  P	1 4	2q-1	q

  A． 1 12

  B． 7 12

  C． 1 2

  D． 1 3
  组卷：921引用：6难度：0.9

  解析

• 4．曲线y=2x-x³在x=-1处的切线方程为（　　）

  A．x-y+2=0

  B．x+y-2=0

  C．x+y+2=0

  D．x-y-2=0
  组卷：12引用：4难度：0.9

  解析

• 5．已知

  A

  2

  n

  =

  C

  n

  -

  3

  n

  ，则n=（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：153引用：9难度：0.8

  解析

• 6．某地区气象台统计，该地区下雨的概率是

  4

  15

  ，刮风的概率为

  2

  15

  ，既刮风又下雨的概率为

  1

  10

  ，则在刮风天里，下雨的概率为（　　）

  A． 8 225

  B． 1 2

  C． 3 8

  D． 3 4
  组卷：1631引用：4难度：0.7

  解析

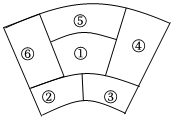• 7．四种不同的颜色涂在如图所示的6个区域，且相邻两个区域不能同色，满足条件的涂法数有（　　）种．

  A．24

  B．72

  C．120

  D．144
  组卷：128引用：2难度：0.7

  解析

四、解答题（本题共6小题，第17题10分，第18-22题每题12分，共70分）

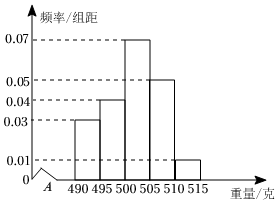• 21．某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上40件作品作为样本称出它们的重量（单位：克），重量的分组区间为（490，495]，（495，500]，⋯，（510，515]，由此得到样本的频率分布直方图，如图所示．
  （Ⅰ）根据频率分布直方图，求重量超过505克的产品数量；
  （Ⅱ）在上述抽取的40件产品中任取2件，设X为重量超过505克的产品数量，求X的分布列和数学期望；
  （Ⅲ）从该流水线上任取5件产品，求恰有2件产品的重量超过505克的概率．
  组卷：51引用：2难度：0.6

  解析

• 22．已知m＞0，e是自然对数的底数，函数f（x）=e^x+m-mln（mx-m）．
  （1）若m=2，求函数

  F

  （

  x

  ）

  =

  e

  x

  +

  x

  2

  2

  -

  4

  x

  +

  2

  -

  f

  （

  x

  ）

  的极值；
  （2）是否存在实数m,∀x＞1，都有f（x）≥0？若存在，求m的取值范围；若不存在，请说明理由．
  组卷：56引用：4难度：0.5

  解析