2022-2023学年河北省张家口市高一(下)期末数学试卷
发布:2024/7/6 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.数据68,70,80,88,89,90,96,98的第30百分位数为( )
组卷:34引用:2难度:0.9 -
2.已知向量
,a满足b,|a|=2,|b|=3,则a•b=1在b上的投影向量为( )a组卷:98引用:6难度:0.7 -
3.已知圆锥的体积为
,底面面积为2π,则该圆锥的侧面积为( )233π组卷:145引用:1难度:0.7 -
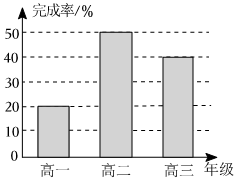 4.某校为了让学生度过一个充实的假期生活,要求每名学生都制定一份假期学习的计划.已知该校高一年级有400人,占全校人数的,高三年级占13,为调查学生计划完成情况,用按比例分配的分层随机抽样的方法从全校的学生中抽取10%作为样本,将结果绘制成如图所示统计图,则样本中高三年级完成计划的人数为( )16组卷:24引用:2难度:0.7
4.某校为了让学生度过一个充实的假期生活,要求每名学生都制定一份假期学习的计划.已知该校高一年级有400人,占全校人数的,高三年级占13,为调查学生计划完成情况,用按比例分配的分层随机抽样的方法从全校的学生中抽取10%作为样本,将结果绘制成如图所示统计图,则样本中高三年级完成计划的人数为( )16组卷:24引用:2难度:0.7 -
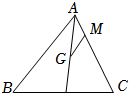 5.在△ABC中,G为△ABC的重心,M为AC上一点,且满足,则( )MC=3AM组卷:1716引用:6难度:0.7
5.在△ABC中,G为△ABC的重心,M为AC上一点,且满足,则( )MC=3AM组卷:1716引用:6难度:0.7 -
6.在三棱锥A-BCD中,∠BAC=∠CAD=∠DAB=40°,AB=AC=AD=2,一只蜗牛从B点出发,绕三棱锥三个侧面爬行一周后,到棱AB的中点E,则蜗牛爬行的最短距离是( )
组卷:48引用:2难度:0.6 -
7.在棱长为2的正方体ABCD-A1B1C1D1中,P,Q是C1D1,B1C1的中点,过点A作平面α,使得平面α∥平面BDPQ,则平面α截正方体所得截面的面积是( )
组卷:85引用:2难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数
.f(x)=4sinx2cos(x2+π3)+3
(1)若,求f(α)=13;cos(α+56π)
(2)若不等式|f2(x)-λ|≤f(x)+2对任意的恒成立,求λ的取值范围.x∈[-π6,π3]组卷:12引用:1难度:0.5 -
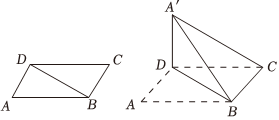 22.如图,在平行四边形ABCD中,∠A=60°,AD=2,AB=4,将△ABD沿BD折起到△A′BD,满足.A′C=25
22.如图,在平行四边形ABCD中,∠A=60°,AD=2,AB=4,将△ABD沿BD折起到△A′BD,满足.A′C=25
(1)求证:平面A′BD⊥平面BCD;
(2)若在线段A′C上存在点M,使得二面角M-BD-C的大小为60°,求此时CM的长度.组卷:69引用:1难度:0.5


