2022-2023学年江苏省盐城市亭湖区景山中学九年级(上)期中数学试卷
发布:2024/9/6 12:0:8
一、选择题(本大题共8小题,每小题3分,共24分)
-
1.下列函数表达式中,一定为二次函数的是( )
组卷:330引用:6难度:0.8 -
2.已知点(-1,y1),(-4,y2)都在y=2x2-3的图象上,则( )
组卷:108引用:4难度:0.6 -
3.一道选择题有四个答案,其中只有一个答案正确,小亮不会做,他随意填上了一个答案,那么他填对的概率是( )
组卷:25引用:5难度:0.7 -
4.若二次函数y=ax2的图象经过点(1,-2),则它也经过( )
组卷:509引用:10难度:0.6 -
5.下列语句中,错误的有( )
①相等的圆心角所对的弧相等;②等弦对等弧;③长度相等的两条弧是等弧;④方程x2-4x+5=0的两个实数根之和为4.组卷:1122引用:7难度:0.5 -
6.五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是( )
组卷:2324引用:28难度:0.5 -
 7.为培养学生动手实践能力,学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中,设置了一个圆形展厅.如图,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是72°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器( )组卷:445引用:6难度:0.6
7.为培养学生动手实践能力,学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中,设置了一个圆形展厅.如图,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是72°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器( )组卷:445引用:6难度:0.6 -
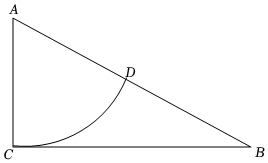 8.可以用如图所示的图形研究方程x2+ax=b2的解:在Rt△ABC中,∠C=90°,AC=,BC=b,以点A为圆心作弧交AB于点D,使AD=AC,则该方程的一个正根是( )a2组卷:1114引用:3难度:0.5
8.可以用如图所示的图形研究方程x2+ax=b2的解:在Rt△ABC中,∠C=90°,AC=,BC=b,以点A为圆心作弧交AB于点D,使AD=AC,则该方程的一个正根是( )a2组卷:1114引用:3难度:0.5
二、填空题(本大题共8小题,每小题3分,共24分)
-
9.方程x2-3=0的根是.
组卷:2462引用:25难度:0.7
三、解答题(本大题共11小题,共102分.解答应写出文字说明、证明过程或演算步骤.)
-
26.【新知】
19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程x2+bx+c=0的几何解法:如图1,在平面直角坐标系中,已知点A(0,1)、B(-b,c),以AB为直径作⊙P.若⊙P交x轴于点M(m,0)、N(n,0),则m、n为方程x2+bx+c=0的两个实数根.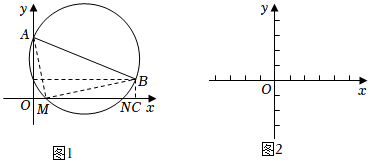
【探究】
(1)由勾股定理得,AM2=12+m2,BM2=c2+(-b-m)2,AB2=(1-c)2+b2.在Rt△ABM中,AM2+BM2=AB2所以12+m2+c2+(-b-m)2=(1-c)2+b2.
化简得:m2+bm+c=0.同理可得:.
所以m、n为方程x2+bx+c=0的两个实数根.
【运用】
(2)在图2中的x轴上画出以方程x2-3x-2=0两根为横坐标的点M、N.
(3)已知点A(0,1)、B(6,9),以AB为直径作⊙C.判断⊙C与x轴的位置关系,并说明理由.
【拓展】
(4)在平面直角坐标系中,已知两点A(0,a)、B(-b,c),若以AB为直径的圆与x轴有两个交点M、N,则以点M、N的横坐标为根的一元二次方程是 .组卷:1882引用:8难度:0.4 -
27.如图1,抛物线y=tx2-16tx+48t(t为常数,t<0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)点A的坐标是 ,点B的坐标是 ;
(2)如图2,点D是抛物线上的一点,且位于第一象限,连接BD,延长BD交y轴于点E,若∠BCE=∠BEC.
①求点D的坐标(用含t的式子表示);
②若以点D为圆心,半径为8作⊙D,试判断⊙D与y轴的位置关系;
(3)若该抛物线经过点(h,),且对于任意实数x,不等式tx2-16tx+48t≤163恒成立,求△BOC外心F与内心I之间的距离.163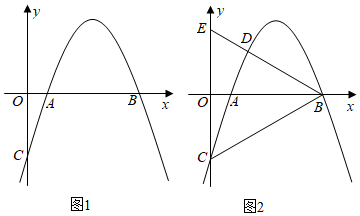 组卷:1018引用:4难度:0.3
组卷:1018引用:4难度:0.3


