【新知】
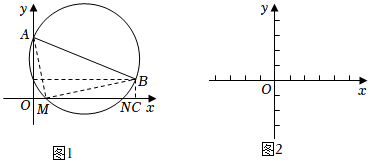
19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程x2+bx+c=0的几何解法：如图1，在平面直角坐标系中，已知点A（0，1）、B（-b,c），以AB为直径作⊙P．若⊙P交x轴于点M（m,0）、N（n,0），则m、n为方程x2+bx+c=0的两个实数根．
【探究】
（1）由勾股定理得，AM2=12+m2，BM2=c2+（-b-m）2，AB2=（1-c）2+b2．在Rt△ABM中，AM2+BM2=AB2所以12+m2+c2+（-b-m）2=（1-c）2+b2．
化简得：m2+bm+c=0．同理可得：n2+bn+c=0n2+bn+c=0．
所以m、n为方程x2+bx+c=0的两个实数根．
【运用】
（2）在图2中的x轴上画出以方程x2-3x-2=0两根为横坐标的点M、N．
（3）已知点A（0，1）、B（6，9），以AB为直径作⊙C．判断⊙C与x轴的位置关系，并说明理由．
【拓展】
（4）在平面直角坐标系中，已知两点A（0，a）、B（-b,c），若以AB为直径的圆与x轴有两个交点M、N，则以点M、N的横坐标为根的一元二次方程是 x2+bx+ac=0x2+bx+ac=0．
【答案】n2+bn+c=0；x2+bx+ac=0
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/6 12:0:8组卷：1873引用：8难度：0.4
相似题
-
1．已知：如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．
（1）试说明直线AC与⊙O的位置关系，并说明理由；
（2）当BD=2，sinC=时，求⊙O的半径．12发布：2024/12/23 8:30:2组卷：292引用：2难度：0.5 -
2．如图，AB是圆O的直径，点C是圆O上一点，点D是弧BC的中点，连接AC、BD，过点D作AC的垂线EF，交AC的延长线于点E，交AB的延长线于点F．
（1）判断直线EF与圆O的位置关系，并说明理由；
（2）若AB=5，BD=3，求线段AE的长．发布：2025/1/28 8:0:2组卷：234引用：1难度：0.5 -
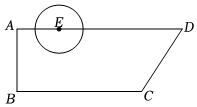3．如图，在直角梯形ABCD中，AD∥BC，∠A=90°，E是AD上一定点，AB=3，BC=6，AD=8，AE=2．点P是BC上一个动点，以P为圆心，PC为半径作⊙P．若⊙P与以E为圆心，1为半径的⊙E有公共点，且⊙P与线段AD只有一个交点，则PC长度的取值范围是 ．发布：2025/1/21 8:0:1组卷：442引用：4难度：0.3
