2023-2024学年江西省宜春市上高二中高三(上)第一次月考数学试卷
发布:2024/9/7 8:0:8
一、单选题(每小题5分,共40分)
-
1.已知集合A={x∈N|1<x≤4},B={x|x2-x-6≤0},则A∩B=( )
组卷:93引用:4难度:0.9 -
2.命题“∀x∈R,x+1≥x”的否定是( )
组卷:11引用:3难度:0.8 -
3.已知命题p:“m=-1”,命题q:“直线x-y=0与直线x+m2y=0互相垂直”,则命题p是命题q的( )
组卷:78引用:9难度:0.9 -
4.已知函数
的定义域是R,则m的取值范围是( )f(x)=1mx2+2mx+1组卷:996引用:14难度:0.5 -
5.在R上定义运算:
,若不等式abcd=ad-bc对任意实数x恒成立,则实数a的最小值为( )x-1a-2a+1x≥1组卷:187引用:8难度:0.7 -
6.在△ABC中,acosA=bcosB,则△ABC的形状为( )
组卷:264引用:31难度:0.7 -
7.已知椭圆E:
的左、右焦点分别为F1,F2,O为坐标原点,若以F1F2为直径的圆与椭圆E在第一象限交于点P,且△OPF2是等边三角形,则椭圆E的离心率为( )x2a2+y2b2=1(a>b>0)组卷:99引用:4难度:0.7
四、解答题(共70分)
-
 21.对于椭圆:,我们称双曲线:y2a2+x2b2=1(a>b>0)为其伴随双曲线.已知椭圆C:y2a2-x2b2=1(y23+x2b2=1),它的离心率是其伴随双曲线Γ离心率的0<b<3倍.22
21.对于椭圆:,我们称双曲线:y2a2+x2b2=1(a>b>0)为其伴随双曲线.已知椭圆C:y2a2-x2b2=1(y23+x2b2=1),它的离心率是其伴随双曲线Γ离心率的0<b<3倍.22
(1)求椭圆C伴随双曲线Γ的方程;
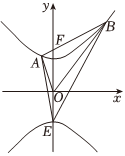
(2)如图,点E,F分别为Γ的下顶点和上焦点,过F的直线l与Γ上支交于A,B两点,设△ABO的面积为S,∠AOB=θ(其中O为坐标原点).若△ABE的面积为,求6+33.Stanθ组卷:159引用:8难度:0.4 -
22.已知函数f(x)=(x2+1)ex-mx-1.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为x-y+n=0,求m,n;
(2)若f(x)在[-1,+∞)上恰有两个不同的零点,求实数m的取值范围.组卷:32引用:2难度:0.5


