2022-2023学年四川省内江六中高二（下）第一次月考数学试卷（文科）

一、单选题（本大题共12小题，共60分。在每小题列出的选项中，选出符合题目的一项）

• 1．命题“∃x＞0，x²-1＞0”的否定是（　　）

  A．∃x≤0，x2-1＞0	B．∃x＞0，x2-1≤0
  C．∀x＞0，x2-1≤0	D．∀x≤0，x2-1＞0
  组卷：78引用：5难度：0.7

  解析

• 2．椭圆

  x

  2

  2

  +

  y

  2

  4

  =

  1

  的离心率是（　　）

  A． 2 2

  B． 2

  C． 6 2

  D． 6 3
  组卷：359引用：4难度：0.8

  解析

• 3．下列说法正确的是（　　）

  A．若p∨q为假命题，则p,q都是假命题

  B．“这棵树真高”是命题

  C．命题“∃x∈R使得x2+2x+3＜0”的否定是：“∀x∈R，x2+2x+3＞0”

  D．在△ABC中，“A＞B”是“sinA＞sinB”的充分不必要条件
  组卷：3引用：1难度：0.8

  解析

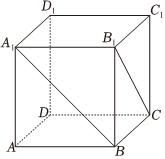• 4．在正方体ABCD-A₁B₁C₁D₁中，异面直线A₁B，B₁C所成角的大小为（　　）
  ​

  A．90°

  B．60°

  C．45°

  D．30°
  组卷：380引用：4难度：0.5

  解析

• 5．已知双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的两条渐近线相互垂直，焦距为12，则该双曲线的虚轴长为（　　）

  A．6

  B． 6 2

  C． 9 2

  D． 12 2
  组卷：409引用：5难度：0.8

  解析

• 6．若直线y=mx+2与焦点在x轴上的椭圆

  x

  2

  9

  +

  y

  2

  n

  =

  1

  总有公共点，则n的取值范围是（　　）

  A．（0，4]	B．（4，9）
  C．[4，9）	D．[4，9）∪（9，+∞）
  组卷：301引用：7难度：0.7

  解析

• 7．已知F₁，F₂分别为双曲线

  x

  2

  4

  -

  y

  2

  5

  =1的左、右焦点，M为双曲线右支上一点，满足MF₁⊥MF₂，则△F₁MF₂的面积为（　　）

  A．5

  B．10

  C． 14

  D．2 14
  组卷：190引用：2难度：0.7

  解析

三、解答题（本大题共6小题，共70分）

• 21．已知双曲线

  x

  2

  4

  -

  y

  2

  16

  =

  1

  ．
  （1）试问过点N（1，1）能否作一条直线与双曲线交于S，T两点，使N为线段ST的中点，如果存在，求出其方程；如果不存在，说明理由；
  （2）直线l：y=kx+m（k≠±2）与双曲线有唯一的公共点M，过点M且与l垂直的直线分别交x轴、y轴于A（x₀，0），B（0，y₀）两点．当点M运动时，求点P（x₀，y₀）的轨迹方程．
  组卷：49引用：4难度：0.4

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  上的点

  A

  （

  1

  ，

  3

  2

  ）

  到左、右焦点F₁，F₂的距离之和为4．
  （1）求椭圆C的方程．
  （2）若在椭圆C上存在两点P，Q，使得直线AP与AQ均与圆

  （

  x

  -

  2

  ）

  2

  +

  （

  y

  -

  3

  2

  ）

  2

  =

  r

  2

  （r＞0）相切，问：直线PQ的斜率是否为定值？若是定值，请求出该定值；若不是定值，请说明理由．
  组卷：17引用：3难度：0.5

  解析