2022-2023学年重庆市三峡名校联盟高二(下)联考数学试卷
发布:2024/7/4 8:0:9
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一项是符合题目要求的。
-
1.下列导数运算正确的是( )
组卷:59引用:2难度:0.8 -
 2.某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉D(10,2)后,下列说法正确的是( )组卷:307引用:10难度:0.7
2.某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉D(10,2)后,下列说法正确的是( )组卷:307引用:10难度:0.7 -
3.在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且
pi=1,则下面四种情形中,对应样本的标准差最大的一组是( )4∑i=1组卷:3457引用:16难度:0.8 -
4.(x+y)(x-2y)6的展开式中x2y5的系数为( )
组卷:93引用:3难度:0.8 -
5.某次考试共有4道单选题,某学生对其中3道题有思路,1道题完全没有思路.有思路的题目每道做对的概率为0.8,没有思路的题目,只好任意猜一个答案,猜对的概率为0.25.若从这4道题中任选2道,则这个学生2道题全做对的概率为( )
组卷:323引用:12难度:0.7 -
6.将甲、乙、丙、丁4名医生随机派往①,②,③三个村庄进行义诊活动,每个村庄至少派1名医生,A表示事件“医生甲派往①村庄”;B表示事件“医生乙派往①村庄”;C表示事件“医生乙派往②村庄”,则( )
组卷:587引用:12难度:0.7 -
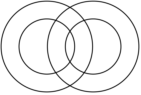 7.如图,4个圆相交共有8个交点,用5种不同的颜色给8个交点染色(5种颜色都用),要求在同一圆上的4个交点的颜色互不相同,则不同的染色方案共有( )种.组卷:74引用:2难度:0.5
7.如图,4个圆相交共有8个交点,用5种不同的颜色给8个交点染色(5种颜色都用),要求在同一圆上的4个交点的颜色互不相同,则不同的染色方案共有( )种.组卷:74引用:2难度:0.5
四、解答题:本题共有6个小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。
-
21.设函数f(x)=ax2+2x-(2a+2)lnx,a∈R.
(1)若函数f(x)存在两个极值点,求实数a的取值范围;
(2)若x∈[1,2]时,不等式f(x)≥0恒成立,求实数a的取值范围.组卷:111引用:4难度:0.5 -
22.已知
有两个极值点x1,x2,且x1<x2.f(x)=xlnx-12ax2+x
(1)若f(x)的极大值大于e2,求a的范围;
(2)若x2>3x1,证明:.x1+x2>2ln3a组卷:36引用:2难度:0.5


