当前位置：试卷中心 > 试卷详情

2023-2024学年河南省济源市英才学校高一（上）期中数学试卷

发布：2024/9/18 2:0:8

1．已知
AB
=
（
3
，-
4
）
，则
|
AB
|
=（　　）
A．25 B．1 C．5 D．12
组卷：131引用：5难度：0.8
解析
2．已知复数
z
=
2
1
-
i
，复数
z
是复数z的共轭复数，则
z
•
z
=（　　）
A．1 B．
2
C．2 D．
2
2
组卷：271引用：6难度：0.8
解析
3．已知
OA
，
OB
不共线，
OP
=
m
OA
+
n
OB
（
m
,
n
∈
R
）
，若P，A，B三点共线，则下列各组数中成立的是（　　）
A．
m
=
1
3
，
n
=
1
2
B．m=1，n=-1 C．m=1，n=2 D．m=2，n=-1
组卷：290引用：3难度：0.8
解析
4．已知|
a
|=
2
，|
b
|=1，且（
a
-2
b
）⊥（2
a
+
b
），则向量
a
与
b
的夹角余弦值是（　　）
A．
3
2
B．
2
3
C．-
1
2
D．-
3
2
组卷：417引用：3难度：0.7
解析
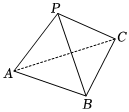
5．如图所示，在三棱锥P-ABC的六条棱所在的直线中，异面直线共有（　　）
A．2对 B．3对 C．4对 D．6对
组卷：450引用：4难度：0.9
解析
6．△ABC的内角A，B，C的对边分别为a,b,c.若b=6，a=2c,
B
=
π
3
，则△ABC的面积为（　　）
A．
2
3
B．
3
3
C．
6
3
D．6
组卷：335引用：11难度：0.7
解析
7．已知a,b,c分别为△ABC三个内角A，B，C的对边，且acosC+bcosA=b,则△ABC是（　　）
A．等腰三角形 B．直角三角形
C．等腰直角三角形 D．等腰或直角三角形
组卷：647引用：12难度：0.7
解析

21．在△ABC中，角A，B，C的对边分别为a,b,c,且
sin
（
π
2
+
C
）
=
2
b
+
c
2
a
．
（1）求角A；
（2）若a=4，△ABC的面积为
4
3
3
，求△ABC的周长．
组卷：82引用：2难度：0.6
解析
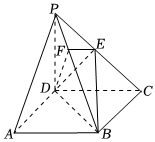22．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
（1）求证：PA∥平面EDB；
（2）求证：PB⊥平面EFD．
组卷：2158引用：12难度：0.6
解析

A．等腰三角形	B．直角三角形
C．等腰直角三角形	D．等腰或直角三角形

1．已知AB=（3，-4），则|AB|=（ ）