2022-2023学年陕西省西安市周至六中高二（下）期中数学试卷（理科）

一、单选题（共12题；共60分）

• 1．复数z满足z（2+i）=3-6i（i为虚数单位），则复数z的虚部为（　　）

  A．3

  B．-3

  C．3i

  D．-3i
  组卷：44引用：9难度：0.9

  解析

• 2．“大自然是懂数学的”，自然界中大量存在如下数列：1，1，2，3，x,8，13，21，…，则其中x的值是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：188引用：2难度：0.9

  解析

• 3．已知函数y=f（x）在x=1处的切线与直线x+y-3=0垂直，则f'（1）=（　　）

  A．2

  B．0

  C．1

  D．-1
  组卷：110引用：4难度：0.8

  解析

• 4．用数学归纳法证明 1+

  1

  2

  +

  1

  3

  +…+

  1

  2

  n

  -

  1

  ＜n（n∈N^*，n＞1）时，第一步应验证不等式（　　）

  A． 1 + 1 2 ＜ 2	B． 1 + 1 2 + 1 3 ＜ 2
  C． 1 + 1 2 + 1 3 ＜ 3	D． 1 + 1 2 + 1 3 + 1 4 ＜ 3
  组卷：1406引用：58难度：0.9

  解析

• 5．若函数y=e^x+mx有极值，则实数m的取值范围是（　　）

  A．m＞0

  B．m＜0

  C．m＞1

  D．m＜1
  组卷：51引用：6难度：0.9

  解析

• 6．将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案种数是（　　）

  A．18种

  B．36种

  C．54种

  D．72种
  组卷：11引用：2难度：0.8

  解析

• 7．关于x的二项式

  （

  2

  x

  -

  1

  x

  ）

  4

  展开式中的常数项是（　　）

  A．24

  B．-24

  C．6

  D．-6
  组卷：44引用：1难度：0.9

  解析

三、解答题（共6题；共70分）

• 21．已知（1+2x）ⁿ的展开式中，第六项和第七项的二项式系数最大．
  （1）求n的值；
  （2）求展开式中系数最大的项．
  组卷：68引用：3难度：0.5

  解析

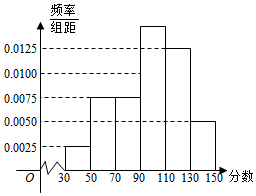• 22．某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，所有学生的成绩均在区间（30，150]内，其频率分布直方图如图．
  （Ⅰ）求获得复赛资格的人数；
  （Ⅱ）从初赛得分在区间（110，150]的参赛者中，利用分层抽样的方法随机抽取7人参加学校座谈交流，那么从得分在区间（110，130]与（130，150]各抽取多少人？
  （Ⅲ）从（Ⅱ）抽取的7人中，选出3人参加全市座谈交流，设X表示得分在区间（130，150]中参加全市座谈交流的人数，求X的分布列及数学期望E（X）．
  组卷：133引用：7难度：0.5

  解析