2022-2023学年全国重点高中新百年竞优联考高三（上）月考数学试卷（理科）（A）

一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．设集合A={x|x=2n-1，n∈N}，B={x|x²-3x-4≤0}，则A∩B=（　　）

  A．{1，3，5}

  B．{-1，1，3}

  C．{-1，1}

  D．{1，3}
  组卷：6引用：1难度：0.9

  解析

• 2．若∃x∈[-2，0]，

  （

  1

  2

  ）

  x

  -2x-a≤0，则实数a的取值范围为（　　）

  A．（-∞，8]

  B．[8，+∞）

  C．（-∞，1]

  D．[1，+∞）
  组卷：11引用：1难度：0.8

  解析

• 3．已知在△ABC中，

  DC

  =

  3

  BD

  ，若

  AB

  =

  m

  AC

  +

  n

  AD

  （m∈R，n∈R），则m-2n=（　　）

  A． 7 3

  B．-3

  C． 1 4

  D． - 5 4
  组卷：9引用：3难度：0.8

  解析

• 4．已知点P（4，3）是角α的终边上一点，则

  tan

  α

  2

  =（　　）

  A． 1 3

  B． ± 1 3

  C．3或 1 3

  D．3
  组卷：70引用：5难度：0.7

  解析

• 5．已知某圆台的上、下底面面积分别为π和4π，高为2，上、下底面的圆周在同一球面上，则该圆台外接球的表面积为（　　）

  A． 116 π 3

  B． 65 π 4

  C． 65 π 16

  D． 65 π 16
  组卷：26引用：1难度：0.5

  解析

• 6．已知数列{a_n}满足a₁=2，且

  （

  n

  +

  1

  ）

  a

  n

  +

  1

  -

  n

  a

  n

  =

  2

  n

  ，则a₄=（　　）

  A．2

  B．4

  C．6

  D．8
  组卷：140引用：4难度：0.7

  解析

• 7．已知S_n为等差数列{a_n}的前n项和，S₂₀₂₀＜S₂₀₂₁，且S₂₀₂₁＞S₂₀₂₂，|a₂₀₂₁|＞|a₂₀₂₂|，则满足S_n＞0的最大的正整数n=（　　）

  A．2021

  B．2022

  C．4042

  D．4043
  组卷：4引用：1难度：0.7

  解析

三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）

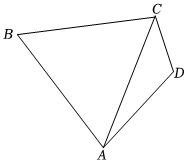• 21．如图所示，在平面四边形ABCD中，

  co

  s

  2

  （

  π

  2

  +

  B

  ）

  +

  cos

  B

  =

  5

  4

  ，AB=AC，AD=2CD=4．
  （1）求角B的大小；
  （2）当角D为何值时，四边形ABCD的面积最大．
  组卷：20引用：2难度：0.5

  解析

• 22．已知函数f（x）=xlnx+x.
  （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
  （2）若g（x）=f（x）-ax²（a∈R）有两个零点x₁，x₂，且x₂＞2x₁，证明：

  x

  2

  1

  +

  x

  2

  2

  ＞

  4

  e

  ．
  组卷：22引用：2难度：0.6

  解析