2022-2023学年上海市嘉定区七年级（下）期末数学试卷

一、选择题：（每题2分，共12分））

• 1．在

  3

  9

  ，

  22

  7

  ，π，

  -

  49

  ，

  0

  .

  23

  ̇

  2

  ，3.1415926，

  27

  中，无理数个数有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：67引用：1难度：0.8

  解析

• 2．下列运算中，正确的是（　　）

  A． （ - 3 ） 2 =-3

  B．- （ - 5 ） 2 =5

  C． a 2 =a

  D． （ - 5 ） 2 =5
  组卷：343引用：6难度：0.9

  解析

• 3．如果一个三角形的两边长分别为3，7，则第三边的长可以是（　　）

  A．3

  B．4

  C．7

  D．10
  组卷：524引用：11难度：0.7

  解析

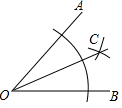• 4．如图，利用尺规作∠AOB的角平分线OC的作法，在用尺规作角平分线时，用到的三角形全等的判定方法是（　　）

  A．SSS

  B．SAS

  C．ASA

  D．AAS
  组卷：237引用：9难度：0.7

  解析

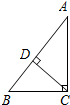• 5．如图，在△ABC中，∠ACB=90°，CD⊥AD，垂足为点D，有下列说法：
  ①点A与点B的距离是线段AB的长；
  ②点A到直线CD的距离是线段AD的长；
  ③线段CD是△ABC边AB上的高；
  ④线段CD是△BCD边BD上的高．
  上述说法中，正确的个数为（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：5670引用：14难度：0.5

  解析

• 6．如图，在△ABC中，点D、E分别在边AB、AC上，BE与CD相交于点O，如果已知∠ABC=∠ACB，补充下列一个条件后，仍无法判定△ABE≌△ACD的是（　　）

  A．AD=AE

  B．BE=CD

  C．OB=OC

  D．∠BDC=∠CEB
  组卷：200引用：4难度：0.7

  解析

二、填空题：（每题2分，共24分）

• 7．

  81

  的平方根是

  ．
  组卷：647引用：16难度：0.8

  解析

• 8．把

  5

  2

  3

  化成幂的形式为

  ．
  组卷：105引用：4难度：0.9

  解析

• 9．比较大小：-4

  -

  17

  （填“＞”、“=”或“＜”）．
  组卷：518引用：8难度：0.8

  解析

四、解答题：（26题15分，27题6分，共21分）

• 26．在△ABC中，∠A=90°，∠BCA=30°，以BC、AC为边向△ABC外作等边△BCD和等边△ACE．
  （1）如图1，连接AD、BE，AD与BE相交于点O．
  ①说明AD=BE的理由．
  ②∠AOB=

  °．（直接填答案）
  （2）如图2，过D作BC的垂线DH，垂足为H，连接DE，交BC于点F，DF与EF相等吗？为什么？
  ​
  组卷：234引用：1难度：0.5

  解析

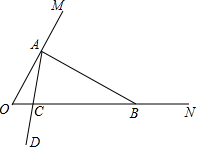• 27．在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“灵动三角形”．例如，三个内角分别为120°、40°、20°的三角形是“灵动三角形”；三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等．如图，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（规定0°＜∠OAC＜90°）．
  （1）∠ABO的度数为

  °，△AOB

  ．（填“是”或“不是”）“灵动三角形”；
  （2）若∠BAC=70°，则△AOC

  （填“是”或“不是”）“灵动三角形”；
  （3）当△ABC为“灵动三角形”时，求∠OAC的度数．
  组卷：3348引用：11难度：0.5

  解析