2023年广东省佛山外国语学校中考数学三模试卷

一、选择题。（每小题3分，共30分）

• 1．据旅游部官网消息，2023年春节7天假日，全国国内出游约308000000人次．数据308000000用科学记数法表示为（　　）

  A．3.08×108

  B．3.08×107

  C．30.8×107

  D．0.308×109
  组卷：138引用：4难度：0.5

  解析

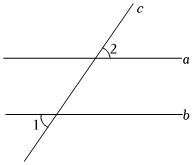• 2．如图，直线c与直线ab都相交．若a∥b,∠1=60°，则∠2=（　　）

  A．60°

  B．55°

  C．50°

  D．45°
  组卷：88引用：2难度：0.9

  解析

• 3．一个不透明的袋子中装有20个小球，其中12个红球，8个绿球，这些小球除颜色外完全相同．从袋子中随机摸出一个小球，则摸出的小球是红球的概率是（　　）

  A． 3 10

  B． 3 8

  C． 2 5

  D． 3 5
  组卷：88引用：6难度：0.7

  解析

• 4．下列运算中，正确的是（　　）

  A．（-b2）3=b6	B．a3+a3=a4
  C．（x+2y）（x-2y）=x2-4y2	D．2a6÷a2=2a3
  组卷：48引用：3难度：0.6

  解析

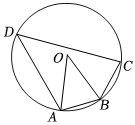• 5．如图，四边形ABCD内接于⊙O，AB=BC，连接OA、OB，∠BAO=70°，则∠D=（　　）

  A．40°

  B．60°

  C．45°

  D．30°
  组卷：362引用：5难度：0.6

  解析

• 6．将y=x²向上平移2个单位后所得的抛物线的解析式为（　　）

  A．y=x2+2

  B．y=x2-2

  C．y=（x+2）2

  D．y=（x-2）2
  组卷：922引用：15难度：0.9

  解析

• 7．如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为35°，若拉线CD的长度是a米，则电线杆AB的长可表示为（　　）

  A．2a•cos35°米	B． 2 a sin 35 ° 米
  C．2a•sin35°米	D． 2 a tan 35 ° 米
  组卷：278引用：4难度：0.5

  解析

• 8．如图，在△ABC 和△DEF中，∠B=∠DEF，AB=DE，添加一个条件后，仍然不能证明△ABC≌△DEF，这个条件可能是（　　）
  ​

  A．∠A=∠D

  B．AC∥DF

  C．BE=CF

  D．AC=DF
  组卷：234引用：1难度：0.5

  解析

三、解答题。（本题有8小题，共72分）

• 23．如图，OA，OB为⊙O的两条半径，直线l与⊙O相切于点B．
  （1）请用无刻度的直尺和圆规过点O作线段OA的垂线（要求：不写作法，保留作图痕迹）；
  （2）连接AB，若（1）中所作垂线分别与AB，直线l交于点C和点D．
  ①求证：∠CBD=∠DCB；
  ②若⊙O的半径为4，cosA=

  4

  5

  ，求OD的长．
  组卷：354引用：7难度：0.7

  解析

• 24．如图，抛物线y=

  1

  2

  x

  2

  +mx+n与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（-4，0），C（0，-2）．
  （1）求抛物线的函数表达式；
  （2）点E是线段AC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDAF的面积最大？求出四边形CDAF的最大面积及此时E点的坐标；
  （3）在y轴上是否存在点P，使得∠OAP+∠OAC=60°？若存在，请直接写出P点的坐标，若不存在，请说明理由．
  组卷：488引用：3难度：0.1

  解析