2023-2024学年福建省厦门市同安区八年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题4分，共40分．每小题都有四个选项，其中有且只有一个选项符合题目要求．）

• 1．第19届亚运会将于2023年9月在杭州举行，下列历届亚运会会徽是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：266引用：15难度：0.9

  解析

• 2．点M（5，2）关于x轴对称的点的坐标为（　　）

  A．（-5，2）

  B．（-5，-2）

  C．（5，-2）

  D．（2，-5）
  组卷：508引用：16难度：0.8

  解析

• 3．小明用长度分别为5，a,9的三根木棒首尾相接组成一个三角形，则a可能的值是（　　）

  A．4

  B．5

  C．14

  D．15
  组卷：48引用：2难度：0.5

  解析

• 4．如图，AD是△ABC的中线，△ABD的面积等于2，则△ABC的面积等于（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：26引用：1难度：0.7

  解析

• 5．若一个多边形的每一个外角都等于45°，则这个多边形是（　　）

  A．五边形

  B．六边形

  C．七边形

  D．八边形
  组卷：809引用：10难度：0.7

  解析

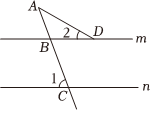• 6．如图，直线m∥n,∠1=70°，∠2=30°，则∠A等于（　　）

  A．30°

  B．35°

  C．40°

  D．50°
  组卷：7370引用：60难度：0.9

  解析

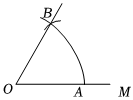• 7．如图，以点O为圆心，任意长为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画出射线OB，则∠AOB=（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：1114引用：14难度：0.7

  解析

• 8．若△ABC是轴对称图形，中线AD所在直线为其唯一的一条对称轴，则下列说法正确的是（　　）

  A．△ABC的周长=3AB	B．△ABC的周长=2AB+BC
  C．△ABC的周长=2BC+AC	D．△ABC的周长=3AD
  组卷：24引用：1难度：0.7

  解析

三、解答题（本大题有9小题，共86分）

• 24．规定：从三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形的三个角分别相等，我们把这条线段叫做这个三角形的“等角分割线”．
  
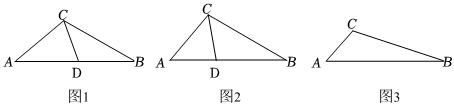
  示例：如图1，在△ABC中，∠ACB=110°，∠A=40°，∠ABC=30°，CD把△ABC分割成△ADC和△CDB两个小三角形，其中，∠CDB=110°，∠DCB=40°，∠ACD=∠ADC=70°．
  ∵∠ACD=∠ADC，
  ∴AC=AD，即△ADC为等腰三角形；
  又∵∠B=∠B，∠DCB=∠A=60°，∠ACB=∠CDB=110°，
  ∴△BDC与△BCA三个角分别相等；
  ∴CD为△ABC的“等角分割线”．
  （1）如图2，在△ABC中，CD为角平分线，∠A=50°，∠B=30°，求证：CD为△ABC的等角分割线；
  （2）在△ABC中，∠A=48°，CD是△ABC的等角分割线，求∠ACB的度数．
  组卷：282引用：3难度：0.5

  解析

• 25．如图1，在平面直角坐标系中，O为坐标原点，点A（8，0），动点P从点A出发以每秒2个单位长度的速度沿线段AO向终点O运动，同时动点Q从点O出发以相同速度沿y轴正半轴运动，点P到达点O时，两点同时停止运动，设运动时间为t秒．
  
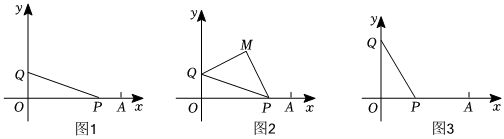
  （1）当t=

  时，∠OPQ=45°；
  （2）如图2，当OP＞OQ时，以PQ为斜边在第一象限作等腰Rt△POM，求M点坐标；
  （3）如图3，当OP＜OQ时，点R是x轴负半轴上一点，且

  OR

  =

  1

  2

  OP

  ，坐标系内有一点N（4-2t,2t-4），求t为何值时，△ONR为等腰直角三角形．
  组卷：103引用：2难度：0.1

  解析