2022-2023学年湖北省荆门外语学校八年级（上）期中数学试卷

一、选择题（3分×10=30分）

• 1．“致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被用于建筑、器物、绘画、标识等作品的设计上，使对称美惊艳了千年的时光．下列大学的校徽图案是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：322引用：18难度：0.9

  解析

• 2．下列各组长度的线段能构成三角形的是（　　）

  A．1cm,2cm,3cm	B．4cm,5cm,10cm
  C．6cm,8cm,10cm	D．5cm,5cm,10cm
  组卷：39引用：3难度：0.7

  解析

• 3．已知点P₁（a-1，5）和点P₂（2，b-1）关于x轴对称，则（a+b）²⁰²²的值为（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：583引用：4难度：0.8

  解析

• 4．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是4：1，这个多边形的边数是（　　）

  A．6

  B．8

  C．9

  D．10
  组卷：187引用：6难度：0.9

  解析

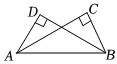• 5．如图，已知∠ADB=∠BCA=90°，添加下列条件后不能使△ABD≌△BAC的是（　　）

  A．AD=BC

  B．AC=BD

  C．∠DAC=∠CBD

  D．∠ABD=∠BAC
  组卷：184引用：7难度：0.7

  解析

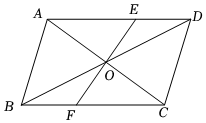• 6．如图，AB∥CD，AD∥BC，AC和BD相交于点O，M，N过点O且与AD，BC分别交于点M，N，则图中全等三角形的组数是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：105引用：5难度：0.6

  解析

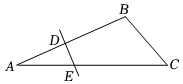• 7．如图，在△ABC中，∠A=23°，线段AB的垂直平分线交AB于点D，交AC于点E，若AE=BC，则∠C的度数是（　　）

  A．30°

  B．45°

  C．46°

  D．60°
  组卷：297引用：2难度：0.7

  解析

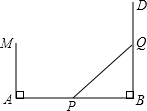• 8．如图，已知线段AB=40米，MA⊥AB于点A，MA=20米，射线BD⊥AB于B，P点从B点向A运动，每秒走1米，Q点从B点向D运动，每秒走3米，P、Q同时从B出发，则出发x秒后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为（　　）

  A．8

  B．8或10

  C．10

  D．6或10
  组卷：1697引用：12难度：0.6

  解析

三、解答题（共72分）

• 23．已知点P是线段MN上一动点，分别以PM，PN为一边，在MN的同侧作△APM，△BPN，并连接BM，AN．
  （Ⅰ）如图1，当PM=AP，PN=BP且∠APM=∠BPN=90°时，试猜想BM，AN之间的数量关系与位置关系，并证明你的猜想；
  （Ⅱ）如图2，当△APM，△BPN都是等边三角形时，（Ⅰ）中BM，AN之间的数量关系是否仍然成立？若成立，请证明你的结论；若不成立，试说明理由．
  （Ⅲ）在（Ⅱ）的条件下，连接AB得到图3，当PN=2PM时，求∠PAB度数．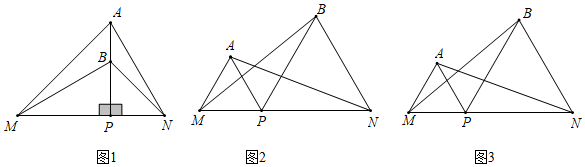
  
  组卷：387引用：6难度：0.2

  解析

• 24．已知直线AB交x轴于点A（a,0），交y轴于点B（0，b），且a、b满足|a+b|+（b-4）²=0．
  （1）求∠ABO的度数；
  （2）如图1，若点C在第一象限，且BE⊥AC于点E，延长BE至点D，使得BD=AC，连接OC、OD、CD，试判断△COD的形状，并说明理由；
  （3）如图2，若点C在OB上，点F在AB的延长线上，且AC=CF，△ACP是以AC为直角边的等腰直角三角形，CQ⊥AF于点Q，求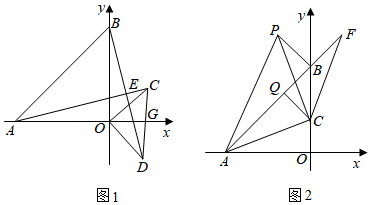

  AF

  -

  2

  BP

  CQ

  的值．
  
  组卷：967引用：4难度：0.3

  解析