当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省大连市甘井子区九年级（上）双基评估数学试卷

发布：2024/7/16 8:0:9

一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有1个选项是正确的）

1．
5
+
1
2
的相反数是（　　）
A．
5
+
1
2
B．
-
5
-
1
2
C．
1
-
5
2
D．
5
-
1
2
组卷：49引用：2难度：0.5
解析
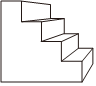2．如图为一个楼梯的左视图，则它的正视图是（　　）
A． B． C． D．
组卷：9引用：2难度：0.5
解析
3．将点P（-1，3）以原点O为旋转中心顺时针旋转90°得到点P'，则点P'所在象限为（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：8引用：2难度：0.5
解析
4．如图，数轴上点Q所表示的数可能是（　　）
A．1.5 B．2.6 C．-0.8 D．-4
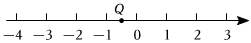组卷：41引用：2难度：0.5
解析
5．若二次根式
b
+
3
b
（b为常数）在实数范围内有意义，则b的取值范围是（　　）
A．b≥-3 B．b＞0 C．b≤3且b≠0 D．b≥-3且b≠0
组卷：16引用：3难度：0.7
解析
6．下列计算错误的是（　　）
A．a³•a⁷=a¹⁰ B．（-5b）²=25b²
C．
（
x
4
）
3
2
=
x
6
D．m⁸÷m²=m⁴
组卷：2引用：2难度：0.7
解析

7．下列说法中正确的一项是（　　）

A．过平面内任意三点即可作一个圆

B．同弦所对的圆周角相等

C．三角函数能够表现现实生活中“周而复始”的变化，具有周期性

D．含有两对等边、一对等角的两个三角形全等

组卷：5引用：2难度：0.5

解析

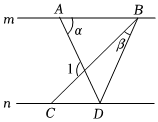8．如图，直线m∥n,BC为∠ABD的三等分线，∠DAB=α，∠DBC=β，则∠1的度数为（　　）
A．α+2β B．2α+β
C．2β+α或
α
+
1
2
β
D．2α+β或2β+α
组卷：664引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

五、解答题（本题共3小题，其中24、25题各11分，26题12分，共34分）

25．综合与实践
问题情境：数学活动课上，王老师出示了一个问题：
如图1，在四边形ABCD中，AB=BC，CH⊥AB，EB⊥BC，∠AGC=∠ABC，∠HCB=∠BDA．在图中找出与∠BAD相等的角，并证明．
独立思考：（1）请解答王老师提出的问题．
实践探究：（2）在原有条件不变的情况下，王老师增加下面的条件，并提出了新问题，请你解答．
“若BD=mAB，AD=aCF，探究线段CF，DF，AC之间的数量关系，并证明（用含有m,a的代数式表示）．”
问题解决：（3）数学活动小组的同学对上述问题进行特殊化研究之后发现，保留（1）条件，如果给出EF，CF，AD之间的数量关系，则图2中所有已经用字母标记的任意两条线段之间的比值均可求．该小组提出下面的问题，请你解答．
“如图2，在（1）的条件下，若EF=kCF（0＜k＜1），AD=3CF，求
GF
BD
的值（用含有k的代数式表示）．”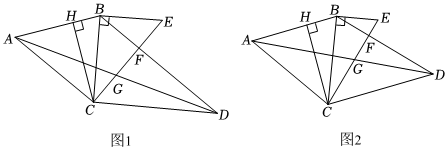
组卷：86引用：2难度：0.5
解析
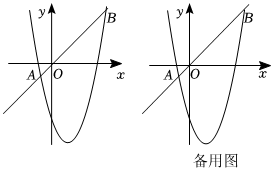26．如图，在平面直角坐标系xOy中，直线y=x与抛物线y=x²+bx+c相交于点A（-1，y_A），B（5，y_B）．
（1）求该抛物线的解析式；
（2）点E在线段OB上，（点E不与点O重合），点F在x轴的正半轴上，∠EFO＜90°，tan∠EFO=
4
3
，设△AEF的面积为S，求S的最大值；
（3）直线y=x与一次函数y=-
1
3
x+b相交于点C，以线段AC为边向直线y=x下方作正方形ACDE．当点E在抛物线内部时，直接写出b的取值范围．
组卷：14引用：2难度：0.5
解析