综合与实践
问题情境：数学活动课上，王老师出示了一个问题：
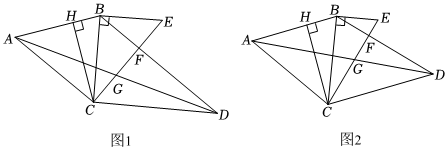
如图1，在四边形ABCD中，AB=BC，CH⊥AB，EB⊥BC，∠AGC=∠ABC，∠HCB=∠BDA．在图中找出与∠BAD相等的角，并证明．
独立思考：（1）请解答王老师提出的问题．
实践探究：（2）在原有条件不变的情况下，王老师增加下面的条件，并提出了新问题，请你解答．
“若BD=mAB，AD=aCF，探究线段CF，DF，AC之间的数量关系，并证明（用含有m,a的代数式表示）．”
问题解决：（3）数学活动小组的同学对上述问题进行特殊化研究之后发现，保留（1）条件，如果给出EF，CF，AD之间的数量关系，则图2中所有已经用字母标记的任意两条线段之间的比值均可求．该小组提出下面的问题，请你解答．
“如图2，在（1）的条件下，若EF=kCF（0＜k＜1），AD=3CF，求GFBD的值（用含有k的代数式表示）．”
GF
BD
【考点】相似形综合题．
【答案】（1）∠BAD=∠BCE=∠EBF，证明见解析过程；
（2）（a-1）2CF2+FD2=m2AC2，证明见解析过程；
（3）．
（2）（a-1）2CF2+FD2=m2AC2，证明见解析过程；
（3）
GF
BD
=
k
k
+
4
k
-
k
3
+
4
k
2
2
k
+
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/16 8:0:9组卷：86引用：2难度：0.5
相似题
-
1．综合与实践
问题情境：如图，在Rt△ABC中，∠ACB=90°，将△ABC绕点B顺时针旋转得到Rt△EBD，连接AE，连接CD并延长交AE于点F．
猜想验证：（1）试猜想△CBD与△ABE是否相似？并证明你的猜想．
探究证明：（2）如图，连接BF交DE于点H，AB与CF相交于点G，是否成立？并说明理由．DHBH=FHEH
拓展延伸：（3）若CD=EF，直接写出的值．BCAB发布：2025/5/23 21:30:2组卷：282引用：3难度：0.2 -
2．如图，在矩形ABCD中，点M、N分别为AD、BC上的点，将矩形ABCD沿MN折叠，使点B落在CD边上的点E处（不与点C，D重合），连接BE，过点M作MH⊥BC于点H．
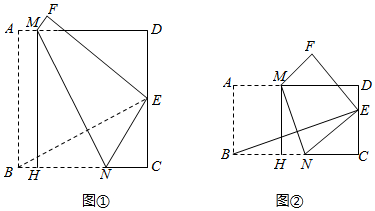
（1）如图①，若BC=AB，求证：△EBC≌△NMH；
（2）如图②，当BC=2AB时，
①求证：△EBC∽△NMH；
②若点E为CD的三等分点，请直接写出的值．AMBN发布：2025/5/23 20:30:1组卷：409引用：2难度：0.2 -
3．在矩形ABCD中，AB=2，AD=4，F是对角线AC上不与点A，C重合的一点，过F作FE⊥AD于E，将△AEF沿EF翻折得到△GEF，点G在射线AD上，连接CG．
（1）如图1，若点A的对称点G落在AD上，∠FGC=90°，延长GF交AB于H，连接CH．
①求证：△CDG∽△GAH；
②求tan∠GHC．
（2）如图2，若点A的对称点G落在AD延长线上，∠GCF=90°，判断△GCF与△AEF是否全等，并说明理由．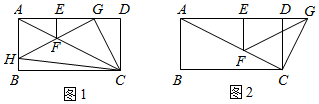
发布：2025/5/23 23:0:1组卷：1132引用：5难度：0.3
