当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省长沙市雅礼中学高三（上）月考数学试卷（一）

发布：2024/8/27 4:0:8

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若集合M={x|log₂x＜4}，N={x|2x≥1}，则M∩N=（　　）
A．{x|0≤x＜8} B．
{
x
|
1
2
≤
x
＜
8
}
C．{x|2≤x＜16} D．
{
x
|
1
2
≤
x
＜
16
}
组卷：139引用：10难度：0.7
解析
2．记等差数列{a_n}的前n项和为S_n，若a₆=16，S₅=35，则{a_n}的公差为（　　）
A．-3 B．-2 C．3 D．2
组卷：631引用：10难度：0.6
解析
3．已知z₁，z₂是关于x的方程x²-2x+2=0的两个根．若z₁=1+i,则|z₂|=（　　）
A．
2
2
B．1 C．
2
D．2
组卷：203引用：7难度：0.7
解析
4．函数
y
=
xsinx
e
|
x
|
的图象大致为（　　）
A． B．
C． D．
组卷：347引用：9难度：0.8
解析
5．已知2x²+kx-m＜0的解集为（t,-1）（t＜-1），则k+m的值为（　　）
A．1 B．2 C．-1 D．-2
组卷：315引用：6难度：0.8
解析
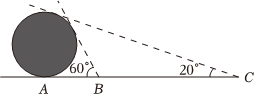6．古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作，也为地图学提供了数学基础．现根据刘徽的《重差》测量一个球体建筑物的高度，已知点A是球体建筑物与水平地面的接触点（切点），地面上B，C两点与点A在同一条直线上，且在点A的同侧．若在B，C处分别测得球体建筑物的最大仰角为60°和20°，且BC=100m,则该球体建筑物的高度约为（　　）（cos10°≈0.985）
A．49.25 m B．50.76 m C．56.74 m D．58.60 m
组卷：734引用：25难度：0.5
解析
7．已知定义域是R的函数f（x）满足：∀x∈R，f（4+x）+f（-x）=0，f（1+x）为偶函数，f（1）=1，则f（2023）=（　　）
A．1 B．-1 C．2 D．-3
组卷：341引用：11难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.

21．已知双曲线
E
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的焦距为10，且经过点
M
（
8
，
3
3
）
．A，B为双曲线E的左、右顶点，P为直线x=2上的动点，连接PA，PB交双曲线E于点C，D（不同于A，B）．
（1）求双曲线E的标准方程．
（2）直线CD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．
组卷：313引用：8难度：0.5
解析
22．设函数
f
（
x
）
=
cosx
-
1
+
x
2
2
（
x
≥
0
）
．
（1）求f（x）的最值；
（2）令g（x）=sinx,g（x）的图象上有一点列
A
i
（
1
2
i
，
g
（
1
2
i
）
）
（
i
=
1
，
2
，…，
n
,
n
∈
N
*
）
，若直线A_iA_i+1的斜率为k_i（i=1，2，…，n-1），证明：
k
1
+
k
2
+
…
+
k
n
-
1
＞
n
-
7
6
．
组卷：64引用：5难度：0.5
解析