2021-2022学年广东省深圳市盐田高级中学高二（上）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．

• 1．直线

  3

  x+y-2=0的倾斜角为（　　）

  A．30°

  B．150°

  C．120°

  D．60°
  组卷：379引用：11难度：0.9

  解析

• 2．方程

  （

  x

  -

  2

  ）

  2

  +

  y

  2

  +

  （

  x

  +

  2

  ）

  2

  +

  y

  2

  =10，化简的结果是（　　）

  A． x 2 25 + y 2 16 =1	B． x 2 25 + y 2 21 =1
  C． x 2 25 + y 2 4 =1	D． y 2 25 + x 2 21 =1
  组卷：585引用：9难度：0.7

  解析

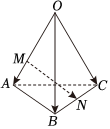• 3．如图，在四面体OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ．点M在OA上，且OM=2MA，N为BC中点，则

  MN

  等于（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  组卷：432引用：74难度：0.7

  解析

• 4．焦点分别为（-2，0），（2，0）且经过点（2，3）的双曲线的标准方程为（　　）

  A．x2- y 2 3 =1

  B． x 2 3 - y 2 = 1

  C．y2- x 2 3 =1

  D． x 2 2 - y 2 2 = 1
  组卷：141引用：7难度：0.9

  解析

• 5．圆x²+y²+2x-4y+3=0的圆心到直线x+y=0的距离为（　　）

  A．2

  B． 2 2

  C．1

  D． 2
  组卷：460引用：8难度：0.8

  解析

• 6．若向量

  a

  =（x,4，5），

  b

  =（1，-2，2），且

  a

  与

  b

  的夹角的余弦值为

  2

  6

  ，则x=（　　）

  A．3

  B．-3

  C．-11

  D．3或-11
  组卷：824引用：8难度：0.9

  解析

• 7．过点（

  2

  ，0）引直线l与曲线y=

  1

  -

  x

  2

  相交于A，B两点，O为坐标原点，当△AOB的面积取最大值时，直线l的斜率等于（　　）

  A． 3 3

  B．- 3 3

  C．± 3 3

  D．- 3
  组卷：651引用：12难度：0.7

  解析

四、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．

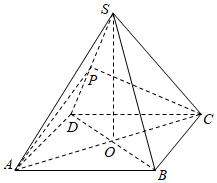• 21．如图，在正四棱锥S一ABCD中，O为顶点S在底面ABCD内的投影，P为侧棱SD的中点且SO=OD．
  （1）证明：SB∥平面PAC；
  （2）求直线BC与平面PAC的所成角的大小．
  组卷：156引用：3难度：0.3

  解析

• 22．已知双曲线E：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的实轴长为2

  2

  ，F为右焦点，M（0，1），N（0，-1），且△MNF为等边三角形．
  （1）求双曲线E的方程；
  （2）过点M的直线l与E的左右两支分别交于P、Q两点，求△PQN面积的取值范围．
  组卷：270引用：2难度：0.6

  解析