2022-2023学年浙江省绍兴市柯桥区联盟八年级（下）期中数学试卷

一、选择题（本题有10小题，每小题2分，共20分）

• 1．下列图标中，属于中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：20引用：1难度：0.9

  解析

• 2．若式子

  x

  -

  2

  x

  -

  3

  有意义，则x的取值范围为（　　）

  A．x≥2

  B．x≠3

  C．x≤2或x≠3

  D．x≥2且x≠3
  组卷：899引用：6难度：0.9

  解析

• 3．下表记录了四位射击运动员选拔比赛成绩的平均数和方差：
  

  运动员	甲	乙	丙	丁
  平均数（环）	9.1	9.2	9.1	9.2
  方差（环2）	3.5	15.5	16.5	3.5

  根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：145引用：4难度：0.8

  解析

• 4．已知四边形ABCD中，∠A-∠C=∠D-∠B，下列说法正确的是（　　）

  A．AB∥CD	B．AD∥CB
  C．AB∥CD 且AD∥CB	D．AB，CD与BC，AD都不平行
  组卷：192引用：4难度：0.8

  解析

• 5．用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（　　）

  A．有一个内角小于90°

  B．每一个内角都大于90°

  C．有一个内角小于或等于90°

  D．每一个内角都小于90°
  组卷：950引用：21难度：0.7

  解析

• 6．如果一个三角形的三边长分别为

  1

  2

  、k、

  7

  2

  ，则化简

  k

  2

  -

  12

  k

  +

  36

  -|2k-5|的结果是（　　）

  A．-k-1

  B．k+1

  C．3k-11

  D．11-3k
  组卷：7332引用：7难度：0.5

  解析

• 7．某景点的门票价格为220元，日接待游客5000人．当门票价格每提高10元，日游客数减少50人．若想每天的门票收入达到138万元，问门票价格需提高多少元？设门票价格提高x元，则可列方程为（　　）

  A．（220+x）（5000-5x）=1380000

  B．（220+x）（5000-5x）=138

  C．（220+x）（5000-50x）=138

  D．（220+x）（5000-50x）=1380000
  组卷：671引用：5难度：0.7

  解析

• 8．已知关于x的一元二次方程x²-x+

  1

  4

  m=0有两个不相等的实数根，设此方程的一个实数根为b,令y=4b²-4b-3m+3，则（　　）

  A．y＞-1

  B．y≥-1

  C．y≤1

  D．y＜1
  组卷：1768引用：9难度：0.6

  解析

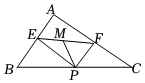• 9．如图，在△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为（　　）

  A．2.5

  B．2.4

  C．1.2

  D．1.3
  组卷：1698引用：11难度：0.5

  解析

三、解答题（本题有7小题，共50分）

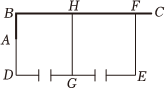• 26．饲养场准备利用现成的一堵“7”字形的墙面（粗线A-B-C表示墙面）建饲养场，已知AB⊥BC，AB=3米，BC=15米，现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF，并在每个区域开一个宽2米的门，如图（细线表示篱笆，饲养场中间用篱笆GH隔开），点F在线段BC上．
  （1）设EF的长为x米，则DE=

  米；（用含x的代数式表示）
  （2）若围成的饲养场BDEF的面积为132平方米，求饲养场的宽EF的长；
  （3）所围成的饲养场BDEF的面积能否为171平方米？如果能达到，求出EF的长；如果不能，请说明理由．
  组卷：627引用：4难度：0.6

  解析

• 27．定义：如果一个凸四边形有三条边相等，那么称这个凸四边形为“准等边四边形”．如正方形就是一个“准等边四边形”．
  （1）如图，在给定的网格中，找到格点D．使得以A、B、C、D为顶点的四边形是准等边四边形．
  （2）如图1，▱ABCD中，对角线CA平分∠BCD，将线段CD绕点C顺时针方向旋转一个角度α（0＜α＜∠B）至CE，连接AE、DE．
  ①求证：四边形ABCE是准等边四边形；
  ②如图2，连接BE，求证：∠BED=∠ACB；
  （3）如图3，在准等边四边形ABCD中，∠C=90°，AB=BC=CD=2，∠B=150°，请求出∠BAD的大小及该四边形的面积．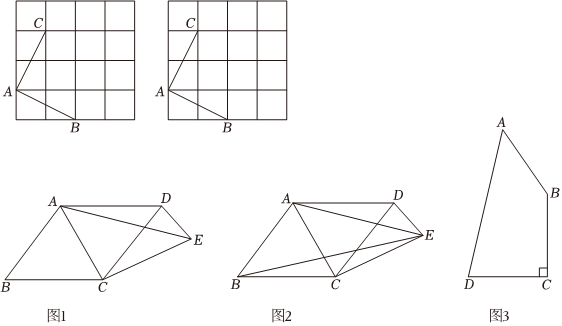
  
  组卷：183引用：1难度：0.2

  解析