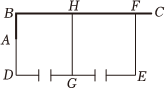
饲养场准备利用现成的一堵“7”字形的墙面（粗线A-B-C表示墙面）建饲养场，已知AB⊥BC，AB=3米，BC=15米，现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF，并在每个区域开一个宽2米的门，如图（细线表示篱笆，饲养场中间用篱笆GH隔开），点F在线段BC上．
（1）设EF的长为x米，则DE=（45-3x）（45-3x）米；（用含x的代数式表示）
（2）若围成的饲养场BDEF的面积为132平方米，求饲养场的宽EF的长；
（3）所围成的饲养场BDEF的面积能否为171平方米？如果能达到，求出EF的长；如果不能，请说明理由．
【考点】一元二次方程的应用．
【答案】（45-3x）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：627引用：4难度：0.6
相似题
-
1．为帮助人民应对疫情，某药厂下调药品的价格．某种药品经过连续两次降价后，由每盒200元下调至128元，已知每次下降的百分率相同．
（1）求这种药品每次降价的百分率是多少？
（2）已知这种药品的成本为100元，若按此降价幅度再一次降价，药厂是否亏本？发布：2025/6/18 6:0:1组卷：978引用：13难度：0.8 -
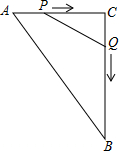2．如图，在△ABC中，AC=50m,BC=70m,∠C=90°，点P从点A开始沿AC边向点C以2m/s的速度匀速移动，同时另一点Q由点C开始以3m/s的速度沿着射线CB匀速移动，当△PCQ的面积等于300m2时，运动时间为（ ）发布：2025/6/18 9:0:1组卷：265引用：2难度：0.7 -
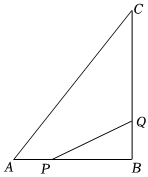3．如图所示，△ABC中，∠B=90°，AB=6cm,BC=8cm.
（1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P、Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．
（2）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P、Q同时出发，问几秒后，△PBQ的面积为1cm2？发布：2025/6/18 9:0:1组卷：2247引用：10难度：0.1
