2022-2023学年湖北省新高考联考协作体高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知i是虚数单位，复数z=2+i,则

  z

  •

  i

  的虚部为（　　）

  A．1

  B．2

  C．i

  D．2i
  组卷：41引用：2难度：0.8

  解析

• 2．某中学高一年级有20个班，每班50人；高二年级有24个班，每班45人．甲就读于高一，乙就读于高二．学校计划从这两个年级中共抽取208人进行视力调查，若采用分层抽样的方式进行抽样，则下列说法：①甲乙两人可能同时被抽取；②高一、高二年级分别抽取100人和108人；③乙被抽到的可能性比甲的大．其中正确的有（　　）

  A．①

  B．①③

  C．①②

  D．①②③
  组卷：58引用：3难度：0.8

  解析

• 3．已知α，β是两个不同的平面，m为平面α内的一条直线，下列说法正确的是（　　）

  A．若m∥β，则α∥β	B．若l⊂β，m∥l,则m∥β
  C．若α⊥β，则m⊥β	D．若m⊥β，则α⊥β
  组卷：75引用：5难度：0.5

  解析

• 4．已知向量

  a

  ，

  b

  满足

  |

  b

  |

  =

  1

  ，

  a

  ⊥

  b

  ，则

  a

  -

  2

  b

  在

  b

  方向上的投影向量为（　　）

  A．2

  B． 2 a

  C． - 2 b

  D．-2
  组卷：340引用：8难度：0.9

  解析

• 5．已知α，β，γ是三个平面，α∩β=l₁，α∩γ=l₂，β∩γ=l₃，则下列结论正确的是（　　）

  A．直线l2与直线l3可能是异面直线

  B．若l1∩l2=O，则直线l1与直线l3可能平行

  C．若l1∩l2=O，则直线l2与直线l3不可能相交于O点

  D．若l1∥l2，则l1∥l3
  组卷：52引用：2难度：0.6

  解析

• 6．已知平面向量

  a

  ，

  b

  ，

  c

  满足

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  且对∀t∈R，有

  |

  b

  +

  t

  a

  |

  ≥

  |

  b

  -

  a

  |

  恒成立，则

  2

  a

  -

  b

  与

  b

  的夹角为（　　）

  A． 2 π 3

  B． π 2

  C． π 3

  D． π 6
  组卷：276引用：4难度：0.5

  解析

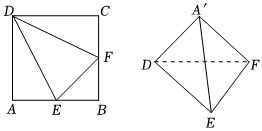• 7．在边长为2的正方形ABCD中，E是AB的中点，点F是BC的中点，将△AED，△BEF，△DCF分别沿DE，EF，DF折起，使A，B，C三点重合于点A′，则A′到平面EFD的距离为（　　）

  A．1

  B． 2 3

  C． 4 3

  D．2
  组卷：106引用：5难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

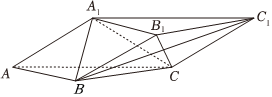• 21．在三棱柱ABC-A₁B₁C₁中，AB=BC=AA₁=2，

  B

  C

  1

  =

  14

  ，

  ∠

  ABC

  =

  2

  π

  3

  ，A₁C₁⊥A₁B．
  （1）证明：平面A₁AC⊥平面ABC；
  （2）求二面角A-A₁B-C的平面角的余弦值．
  组卷：160引用：3难度：0.5

  解析

• 22．记△ABC的内角A，B，C的对边分别为a,b,c,且边BC上的高

  h

  =

  3

  4

  a

  ．
  （1）若

  A

  =

  π

  2

  ，求B；
  （2）已知△ABC中角B和C是锐角，求tanB+4tanC的最小值．
  组卷：90引用：2难度：0.6

  解析