2023-2024学年广东省东莞中学松山湖学校高二（上）第一次段考数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.

• 1．直线

  3

  x

  -

  y

  +

  2

  =

  0

  的倾斜角α是（　　）

  A． π 3

  B． π 6

  C． 2 π 3

  D． - π 3
  组卷：12引用：5难度：0.9

  解析

• 2．已知点P（-3，-4），Q是圆O：x²+y²=4上的动点，则线段PQ长的最小值为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：159引用：2难度：0.8

  解析

• 3．中国是世界上最古老的文明中心之一，中国古代对世界上最重要的贡献之一就是发明了瓷器，中国陶瓷是世界上独一无二的．它的发展过程蕴藏着十分丰富的科学和艺术，陶瓷形状各式各样，从不同角度诠释了数学中几何的形式之美．现有一椭圆形明代瓷盘，经测量得到图中数据，则该椭圆瓷盘的焦距为（　　）

  A． 8 3

  B． 2 3

  C． 4 3

  D．4
  组卷：176引用：12难度：0.6

  解析

• 4．已知正方体ABCD-A₁B₁C₁D₁，下列向量的数量积不为0的是（　　）
  

  A． A D 1 • B 1 C

  B． B D 1 • AC

  C． B D 1 • BC

  D． AB • A D 1
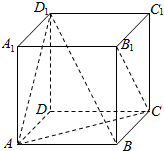  组卷：25引用：3难度：0.7

  解析

• 5．过点P（3，2）且在两坐标轴上的截距相等的直线方程为（　　）

  A．x-y-1=0或y=0	B．x+y-5=0或2x-3y=0
  C．x+y-5=0或y=0	D．x-y-1=0或2x-3y=0
  组卷：178引用：6难度：0.6

  解析

• 6．已知圆O₁：（x+1）²+（y-3）²=9，圆O₂：x²+y²-4x+2y-11=0，则这两个圆的公共弦长为（　　）

  A． 24 5

  B． 12 5

  C． 9 5

  D． 1 5
  组卷：57引用：8难度：0.7

  解析

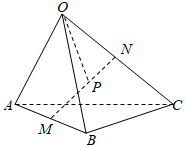• 7．已知三棱锥O-ABC，点M，N分别为边AB，OC的中点，P是MN上的点，满足

  MP

  =2

  PN

  ，设

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，则

  OP

  等于（　　）

  A． 1 6 a + 1 6 b - 1 3 c	B． 1 6 a + 1 3 a + 1 6 c
  C． 1 3 a + 1 6 b + 1 6 c	D． 1 6 a + 1 6 b + 1 3 c
  组卷：67引用：2难度：0.8

  解析

四、解答题：本大题共6小题，第17题10分，18、19、20、21、22题各12分，共70分.

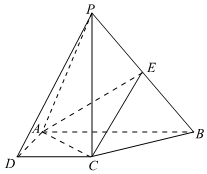• 21．如图所示，在四棱锥P-ABCD中，PC⊥底面ABCD，ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，E是PB的中点．
  （1）求证：平面EAC⊥平面PBC；
  （2）若二面角P-AC-E的余弦值为

  6

  3

  ，求直线PA与平面EAC所成角的正弦值．
  组卷：375引用：12难度：0.5

  解析

• 22．已知直线l：y=kx+b（0＜b＜1）和圆O：x²+y²=1相交于A，B两点．
  （1）当k=0时，过点A，B分别作圆O的两条切线，两切线的交点坐标．
  （2）对于任意的实数k,在y轴上是否存在一点N，满足∠ONA=∠ONB？若存在，请求出此点坐标；若不存在，说明理由．
  组卷：28引用：2难度：0.6

  解析