2022-2023学年安徽省六安二中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．若复数z满足i•z=3-4i,则|z|=（　　）

  A． 10

  B．5

  C．7

  D．25
  组卷：117引用：3难度：0.8

  解析

• 2．围绕民宿目的地进行吃住娱乐闭环消费已经成为疫情之后人们出游的新潮流．在用户出行旅游决策中，某机构调查了某地区1000户偏爱酒店的用户与1000户偏爱民宿的用户住宿决策依赖的出行旅游决策平台，得到统计图，则下列说法中不正确的是（　　）

  A．偏爱民宿用户对小红书平台依赖度最高

  B．在被调查的两种用户住宿决策中，小红书与携程旅行的占比总和相等

  C．小红书在所有被调查用户住宿决策中的占比与携程旅行在所有被调查用户住宿决策中的占比不相等

  D．在被调查的两种用户住宿决策中，同程旅行占比都比抖音的占比高
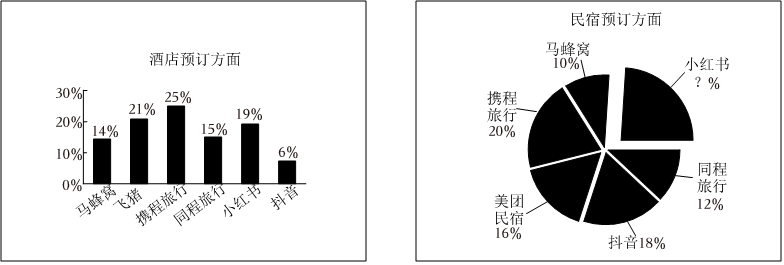  组卷：59引用：4难度：0.7

  解析

• 3．在△ABC中，角A、B、C所对的边分别为a、b、c.已知

  a

  =

  3

  b

  ，A=2B，则A的值是（　　）

  A． π 3

  B． 2 π 3

  C． π 6

  D． 5 π 6
  组卷：270引用：2难度：0.5

  解析

• 4．样本中共有5个个体．其值分别为a,0，1，2，3．若该样本的平均值为1，则样本的标准差为（　　）

  A． 6 5

  B． 6 5

  C．2

  D． 2
  组卷：256引用：9难度：0.9

  解析

• 5．已知圆锥的母线长为2，轴截面顶角的正弦值是

  1

  2

  ，过圆锥的母线作截面，则截面面积的最大值是（　　）

  A．1

  B． 3

  C．1 或 2

  D．2
  组卷：121引用：3难度：0.7

  解析

• 6．对于函数f（x）=2sinx（cosx-sinx）+1，下列结论中正确的是（　　）

  A．f（x）的最大值为 2 2 + 1

  B．f（x）的图象可由 y = 2 cos 2 x 的图象向右平移 π 4 个单位长度得到

  C．f（x）在 （ π 4 ， 3 π 8 ） 上单调递减

  D．f（x）的图象关于点 （ π 8 ， 1 ） 中心对称
  组卷：107引用：3难度：0.6

  解析

• 7．如图，S是△ABC所在平面外一点，AB=BC=2，∠ABC=120°，且SA⊥面ABC，SA=3，则SA与平面SBC的夹角为（　　）

  A． π 3

  B． π 4

  C． π 6

  D． 5 π 6
  组卷：224引用：3难度：0.4

  解析

四、解答题：本题共6小题，共70分.解答须写出文字说明、证明过程和演算步骤。

• 21．如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC=2BC，E为AB的中点，沿DE将△ADE折起，使得点A到点P的位置，且PE⊥EB，M为PB的中点，N是BC上的中点．
  ​
  （1）证明：平面EMN⊥平面PBC；
  （2）求二面角B-EN-M的正切值．
  组卷：223引用：7难度：0.5

  解析

• 22．甲、乙、丙三人进行羽毛球比赛，约定赛制如下：
  累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空：每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束．已知在每场比赛中，甲胜乙和甲胜丙的概率均为

  2

  3

  ，乙胜丙的概率为

  1

  2

  ，各场比赛的结果相互独立．经抽签，第一场比赛甲轮空．
  （1）求前三场比赛结束后，丙被淘汰的概率；
  （2）求只需四场比赛就决出冠军的概率；
  （3）求甲最终获胜的概率．
  组卷：276引用：2难度：0.5

  解析