当前位置：试卷中心 > 试卷详情

2023年辽宁省朝阳市朝阳县部分学校中考数学四模试卷

发布：2024/6/8 8:0:9

一、选择题。（本大题共10小题，每小题3分，共30分）

1．在-2，
1
2
，0，-1这四个数中，最小的数是（　　）
A．-2 B．
1
2
C．0 D．-1
组卷：198引用：5难度：0.9
解析
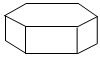2．如图所示的正六棱柱的主视图是（　　）
A． B． C． D．
组卷：104引用：7难度：0.8
解析
3．下列运算中，正确的是（　　）
A．a²•a⁵=a¹⁰ B．（a-b）²=a²-b²
C．（-3a³）²=6a⁶ D．-3a²b+2a²b=-a²b
组卷：1326引用：30难度：0.5
解析

4．下列说法正确的是（　　）

A．为了解人造卫星的设备零件的质量情况，选择抽样调查

B．方差是刻画数据波动程度的量

C．购买一张体育彩票必中奖，是不可能事件

D．掷一枚质地均匀的硬币，正面朝上的概率为1

组卷：435引用：8难度：0.8

解析

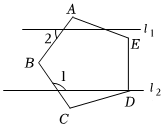5．如图，五边形ABCDE是正五边形，若l₁∥l₂，则∠1-∠2=（　　）
A．72° B．36° C．45° D．47°
组卷：822引用：7难度：0.6
解析
6．有一个正方体木块，每一块的各面都写上不同的数字，三块的写法完全相同，现把它们摆放成如图所示的位置．请你判断数字4对面的数字是（　　）
A．6 B．3 C．2 D．1
组卷：1157引用：15难度：0.7
解析
7．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（-2，5）的对应点A′的坐标是（　　）
A．（2，5） B．（5，2） C．（2，-5） D．（5，-2）
组卷：5770引用：38难度：0.7
解析
8．2022年4月21日中国航天日某校举办了以“航天点亮梦想”为主题的中学生知识竞赛中，五位评委分别给甲队、乙队两组选手的评分如下：
甲组：8，7，9，8，8；乙组：7，9，6，9，9．
则下列说法：①从甲、乙得分的平均分看，他们两人的成绩没有差别；②从甲、乙得分的众数看，乙的成绩比甲好；③从甲、乙得分的中位数看，乙的成绩比甲好；④从甲、乙成绩的稳定性看，乙的成绩比甲好；正确的是（　　）
A．①② B．①③ C．①②③ D．①②③④
组卷：102引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题。（本大题共9小题，满分72分，解答应写出必要的演算步骤、文字说明或证明过程）

24．【问题情境】
（1）王老师给爱好学习的小明和小颖提出这样一个问题：一个问题：如图①，在△ABC中，AB=AC，P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．（不需要证明）
小明的证明思路是：
如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
小颖的证明思路是：
如图②，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
【变式探究】
（2）如图③，当点P在BC延长线上时，问题情境中，其余条件不变，求证：PD-PE=CF．
【结论运用】
（3）如图④，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点 C 处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BG，垂足分别为G，H，若AD=8，CF=3，求PG+PH的值．
【迁移拓展】
（4）图⑤是一个机器模型的截面示意图，在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且AD•CE=DE•BC，
AB
=
2
13
cm
，AD=3cm,
BD
=
37
cm
，MN分别为AE，BE的中点，连接DM，CN，请直接写出△DEM与△CEN的周长之和．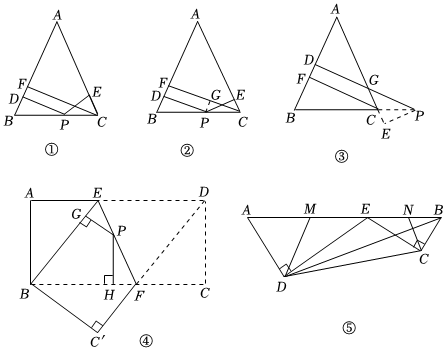

组卷：229引用：1难度：0.5
解析
25．如图1，抛物线y=ax²+bx+3与x轴交于点A（-1，0）、B（3，0），与y轴交于点C，点D为抛物线的顶点．
（1）求抛物线的解析式及顶点D的坐标；
（2）如图2，连接BD，F为x轴上一点，连接CF交BD于点E，当BE=CE时，求点F的坐标；
（3）如图3，连接AC、BC，在（1）中的抛物线上是否存在点G，使得∠BCG=∠ACO？若存在，直接写出点G的坐标；若不存在，请说明理由．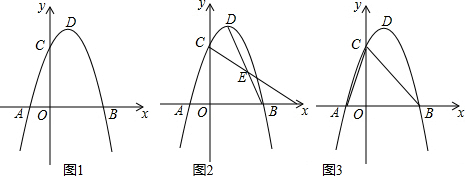
组卷：541引用：2难度：0.7
解析