【问题情境】
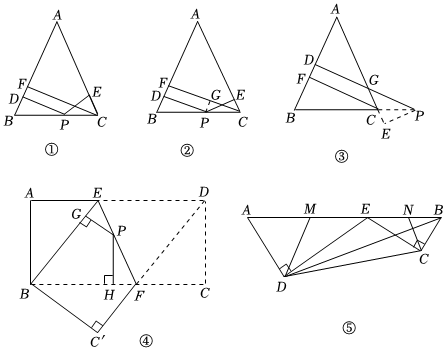
(1)王老师给爱好学习的小明和小颖提出这样一个问题:一个问题:如图①,在△ABC中,AB=AC,P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.(不需要证明)
小明的证明思路是:
如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小颖的证明思路是:
如图②,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】
(2)如图③,当点P在BC延长线上时,问题情境中,其余条件不变,求证:PD-PE=CF.
【结论运用】
(3)如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点 C 处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BG,垂足分别为G,H,若AD=8,CF=3,求PG+PH的值.
【迁移拓展】
(4)图⑤是一个机器模型的截面示意图,在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D,C,且AD•CE=DE•BC,AB=213cm,AD=3cm,BD=37cm,MN分别为AE,BE的中点,连接DM,CN,请直接写出△DEM与△CEN的周长之和.
AB
=
2
13
cm
BD
=
37
cm
【考点】相似形综合题.
【答案】(1)证明见解答过程;
(2)证明见解答过程;
(3)PG+PH的值为4;
(4)(6+2)dm.
(2)证明见解答过程;
(3)PG+PH的值为4;
(4)(6+2
13
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/29 8:0:9组卷:229引用:1难度:0.5
相似题
-
1.(1)阅读解决
华罗庚是我国著名的数学家,他推广的优选法,就是以黄金分割法为指导,用最可能少的试验次数,尽快找到生产和科学实验中最优方案的一种科学试验方法.
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,这个比例被公认为最能引起美感的比例,因此被称为黄金分割.
如图①,点B把线段AC分成两部分,如果=BCAB,那么称点B为线段AC的黄金分割点,它们的比值为ABAC.5-12
在图①中,若AB=12m,则BC的长为 cm;
(2)问题解决
如图②,用边长为40m的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点为H,折痕为CG.
证明:G是AB的黄金分割点;
(3)拓展探究
如图③在边长为m的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF,CB交于点P.发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想这一发现,并说明理由,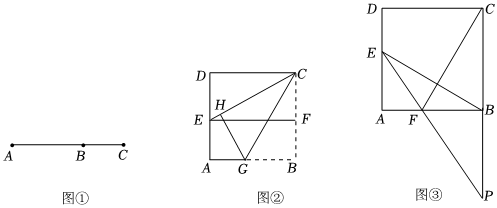 发布:2025/5/25 8:0:2组卷:188引用:1难度:0.3
发布:2025/5/25 8:0:2组卷:188引用:1难度:0.3 -
 2.【了解概念】
2.【了解概念】
在凸四边形中,若一边与它的两条邻边组成的两个内角相等,则称该四边形为邻等四边形,这条边叫做这个四边形的邻等边.
【理解运用】
(1)邻等四边形ABCD中,∠A=30°,∠B=70°,则∠C的度数为.
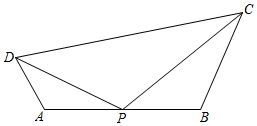
(2)如图,凸四边形ABCD中,P为AB边的中点,△ADP∽△PDC,判断四边形ABCD是否为邻等四边形;并证明你的结论;
【拓展提升】
(3)在平面直角坐标系中,AB为邻等四边形ABCD的邻等边,且AB边与x轴重合,已知A(-1,0),C(m,2),D(2,33),若在边AB上使∠DPC=∠BAD的点P有且仅有1个,请直接写出m的值.3发布:2025/5/25 5:30:2组卷:860引用:3难度:0.3 -
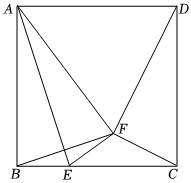 3.已知正方形ABCD中,AB=a.E是BC边上一点(不与B,C重合),BE=b,连接AE,作点B关于AE的对称点F.连接AF,BF,CF,DF.
3.已知正方形ABCD中,AB=a.E是BC边上一点(不与B,C重合),BE=b,连接AE,作点B关于AE的对称点F.连接AF,BF,CF,DF.
(1)求∠BFD的度数.
(2)当△DFC是直角三角形时,求证:BF是CF和DF的比例中项.
(3)在(2)的条件下,求tan∠FDC以及a:b的值.发布:2025/5/25 9:0:1组卷:249引用:1难度:0.3


