2022-2023学年云南省大理州大理市下关一中教育集团高二（上）段考数学试卷（二）（A卷）

一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若i（1-z）=1，则z+

  z

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：5665引用：18难度：0.9

  解析

• 2．直线

  3

  x+y+2=0的倾斜角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：13引用：1难度：0.9

  解析

• 3．在等差数列{a_n}中，已知a₁=2，a₃=8，则a₄+a₅+a₆等于（　　）

  A．40

  B．42

  C．43

  D．45
  组卷：30引用：5难度：0.8

  解析

• 4．在等比数列{a_n}中，a₃，a₁₅是方程x²+6x+2=0的根，则

  a

  2

  a

  16

  a

  9

  的值为（　　）

  A．- 2 + 2 2

  B． - 2

  C． 2

  D． - 2 或 2
  组卷：302引用：14难度：0.7

  解析

• 5．数学家蒙日发现：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，且圆半径的平方等于长半轴、短半轴的平方和，此圆被命名为该椭圆的蒙日圆．若圆

  x

  2

  12

  +

  y

  2

  b

  2

  =

  1

  的蒙日圆为x²+y²=20，则该椭圆的离心率为（　　）

  A． 3 3

  B． 1 3

  C． 2 3

  D． 6 3
  组卷：53引用：4难度：0.7

  解析

• 6．已知抛物线型拱桥的顶点距水面2米时，测量得水面宽8米．当水面升高0.5米后，水面宽度是（　　）米

  A．3

  B．4

  C． 3 3

  D． 4 3
  组卷：54引用：4难度：0.7

  解析

• 7．已知双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦点为

  F

  （

  4

  3

  ，

  0

  ）

  ，过F和P（0，2b）两点的直线与双曲线的一条渐近线平行，则该双曲线的方程为（　　）

  A． x 2 36 - y 2 12 = 1	B． x 2 12 - y 2 36 = 1
  C． x 2 16 - y 2 32 = 1	D． x 2 32 - y 2 16 = 1
  组卷：1引用：3难度：0.5

  解析

四、解答题（共70分.解答应写出文字说明，证明过程或演算步骤）

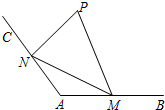• 21．如图，为方便市民游览市民中心附近的“网红桥”，现准备在河岸一侧建造一个观景台P，已知射线AB，AC为两边夹角为120°的公路（长度均超过3千米），在两条公路AB，AC上分别设立游客上下点M，N，从观景台P到M，N建造两条观光线路PM，PN，测得AM=

  3

  千米，AN=

  3

  千米．
  （1）求线段MN的长度；
  （2）若∠MPN=60°，求两条观光线路PM与PN所围成△PMN的面积的最大值．
  组卷：62引用：3难度：0.7

  解析

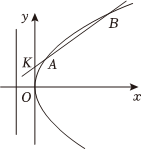• 22．设抛物线y²=2px（p＞0）的准线为l,A、B为抛物线上两动点，AA'⊥l于A'，定点K（0，1）使|KA|+|AA'|有最小值

  2

  ．
  （1）求抛物线的方程；
  （2）当

  KA

  =

  λ

  KB

  （λ∈R且λ≠1）时，是否存在一定点T满足

  TA

  •

  TB

  为定值？若存在，求出T的坐标和该定值；若不存在，请说明理由．
  组卷：97引用：4难度：0.5

  解析