当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省宿迁市泗阳县七年级（上）期中数学试卷

发布：2024/7/26 8:0:9

一、选择题（本大题共12小题，每小题3分，共36分，每小题只有一一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置）

1．若气温上升2℃记作+2℃，则气温下降3℃记作（　　）
A．-2℃ B．+2℃ C．-3℃ D．+3℃
组卷：2946引用：41难度：0.9
解析
2．单项式-5ab的系数是（　　）
A．-5 B．5 C．2 D．1
组卷：94引用：2难度：0.8
解析
3．下列数中，-4的相反数是（　　）
A．4 B．-4 C．
1
4
D．-
1
4
组卷：441引用：9难度：0.9
解析
4．下列式子中：-a,-
2
3
abc,x-y,
3
x
，8x²-7x+2，整式有（　　）
A．2个 B．3个 C．4个 D．5个
组卷：190引用：2难度：0.7
解析
5．介于3和π之间的一个无理数是（　　）
A．
3
+
π
2
B．3.15 C．3.1 D．π-0.15
组卷：335引用：2难度：0.8
解析
6．若数轴上表示数a-1和a+5的点到原点的距离相等，则a的值为（　　）
A．-2 B．-1 C．1 D．2
组卷：851引用：4难度：0.8
解析
7．计算：3x⁶-2x⁶的结果是（　　）
A．-5x⁶ B．5x⁶ C．-x⁶ D．x⁶
组卷：218引用：4难度：0.8
解析
8．式子|x-2|+1的最小值是（　　）
A．0 B．1 C．2 D．3
组卷：3968引用：16难度：0.8
解析
9．如果整式x^n-2+5x-2是三次三项式，那么n等于（　　）
A．3 B．4 C．5 D．6
组卷：1226引用：7难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，共82分，解答时应写出必要的步骤、过程或文字说明）

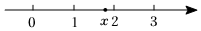27．设a、b都表示有理数，规定一种新运算“※”：当a≥b时，a※b=b²；当a＜b时，a※b=2×a.例如：1※2=2×1=2；3※（-2）=（-2）²=4．
（1）（-1）※（-5）=
；
（2）求（2※3）※（-1）的值；
（3）若有理数x在数轴上对应点的位置如图所示，设：m=（1※x）※x；n=x※3，比较m、n的大小关系．
组卷：177引用：1难度：0.5
解析
28．问题背景：
初一某数学兴趣小组决定对课本63页第17题进行探索研究，问题如下：
“在钟面上的12个数前面，恰当地添上正号或负号，使它们的和为0，你能做到吗？请与同学交流”
（1）探究一：小王同学首先将所有的数前面都添上正号
①这12个正数的和=
．
②小王发现，取连续2个数相加，当和为9时，则这两个数分别为4，5；而当和为13时，则这两个数可能是12，1或6，7；问：若取连续3个数相加，当和为24时，则这三个数可能是
；
（2）探究二：小赵同学在12个数字前面随机添上6个正号和6个负号，小赵发现，若取连续4个数相加，它们的和总是偶数，并且最大的和为32，而最小的和为-30，和的绝对值最小的是0，则这12个数的和是多少？
（3）探究三：胡老师让小张、小李两位位同学分别尝试用不同的方法，将12个数前面恰当地添上正号或负号，使得这12个整数的和恰好都为0，小张同学采用“配对法”，将12个数分成6组：（1，2），（3，4），（5，6），（7，8），（9，10），（11，12）；通过添加正负号让其中三组数的和为1，另外三组数的和为-1；小李采用“奇偶法”，将12个数按奇偶分成两组：（1，3，5，7，9，11），（2，4，6，8，10，12），通过适当地添加正负号，先使所有的奇数的和为0，再让所有的偶数和也为0，这样就可以使这12个数和为0；
①按照小张同学的办法，共有
种不同的添加方法；
A、9
B、15
C、20
D、21
②小李的方法是否可行？如果可行请你写出一种添加的结果，如果不可行，说说你的理由．
组卷：151引用：1难度：0.5
解析