2021-2022学年安徽省亳州市利辛县九年级（上）期末数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）

• 1．抛物线y=-2（x+3）²+1的顶点坐标是（　　）

  A．（-2，1）

  B．（3，1）

  C．（-3，1）

  D．（-2，3）
  组卷：233引用：2难度：0.9

  解析

• 2．已知双曲线经过点（2，5），则它还经过的点是（　　）

  A．（5，-2）

  B．（4，6）

  C．（3，-7）

  D．（-1，-10）
  组卷：72引用：1难度：0.7

  解析

• 3．下列给出长度的四条线段中，是成比例线段的是（　　）

  A．1，2，3，4

  B．1，2，3，6

  C．2，3，4，5

  D．1，3，4，7
  组卷：738引用：6难度：0.7

  解析

• 4．已知tanα=1，则锐角α的取值是（　　）

  A．α=60°

  B．α=45°

  C．α=30°

  D．α=75°
  组卷：369引用：2难度：0.8

  解析

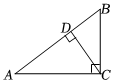• 5．如图，在△ABC中，∠ACB=90°，AC=4，BC=3，CD是△ABC的高，则tan∠BCD的值是（　　）

  A． 4 3

  B． 3 4

  C． 3 5

  D． 4 5
  组卷：777引用：4难度：0.6

  解析

• 6．已知，直线y=-2x+8与双曲线y=-

  4

  x

  相交于点（m,n），则

  1

  m

  +

  2

  n

  的值等于（　　）

  A．-2

  B．2

  C．-4

  D．4
  组卷：274引用：1难度：0.4

  解析

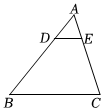• 7．如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，且BC=6，S_{四边形BCED}=8S_△ADE，则DE的长等于（　　）

  A．1.5

  B．2

  C．2.5

  D．3
  组卷：213引用：5难度：0.7

  解析

七、（本题满分12分）

• 22．同学们已经学习了《解直角三角形》的相关知识，掌握了利用锐角三角函数的定义来解决直角三角形的问题，还掌握了通过作高来解决斜三角形（即锐角三角形与钝角三角形）的问题以及相关的实际应用问题．下面请同学们利用这些学习经验，应用类比的方法来解决下面的新问题．
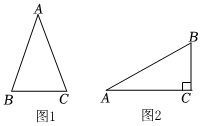
  定义：如图1，在△ABC中，AB=AC，我们称它的腰与底的长度之比为顶角∠A的余对（csdA），记作csdA=

  AB

  BC

  ．
  （1）填空：csd60°=

  ；csd90°=

  ；csd120°=

  ；
  （2）如图2，在Rt△ABC中，∠C=90°，cosA=

  4

  5

  ，求csdA的值．
  组卷：93引用：1难度：0.5

  解析

八、（本题满分14分）

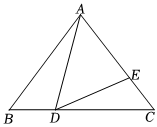• 23．如图，在△ABC中，AB=AC=10，BC=12，点D，E分别在边BC，AC上（点D不与端点B，C重合），并且满足∠ADE=∠B．
  （1）求证：△ABD∽△DCE；
  （2）设BD=x,CE=y,请求出当x取何值时，y取最大值？y的最大值是多少？
  （3）当△ADE是等腰三角形时，求BD的长．
  组卷：864引用：4难度：0.6

  解析