当前位置：试卷中心 > 试卷详情

2022-2023学年江西省宜春市丰城中学高一（下）期中数学试卷

发布：2024/6/20 8:0:9

一、单选题：（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．集合A={x|x²＜9}，B={x∈N|-1＜x＜5}，则A∩B的子集个数为（　　）
A．3 B．2 C．4 D．8
组卷：491引用：5难度：0.7
解析
2．复数z=
i
1
-
i
（i为虚数单位）在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：108引用：12难度：0.9
解析
3．用一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是（　　）
A．圆柱 B．圆锥 C．球 D．圆台
组卷：139引用：8难度：0.8
解析
4．在Rt△ABC中，AC⊥BC，D点是AB边上的中点，BC=6，CA=8，则
AB
•
CD
的值为（　　）
A．-14 B．-6 C．14 D．-12
组卷：76引用：3难度：0.8
解析
5．已知定义在R上的奇函数f（x）满足f（x）=f（2-x）．当1≤x≤2时，f（x）=log₂（x+7），则f（2021）=（　　）
A．3 B．-3 C．-5 D．5
组卷：303引用：4难度：0.8
解析
6．设l₁，l₂，l₃是三条不同的直线，α，β，γ是三个不同的平面，则下列命题是真命题的是（　　）
A．若l₁∥α，α∥l₂，则l₁∥l₂
B．若l₁⊥α，α⊥l₂，则l₁⊥l₂
C．若l₁∥l₂，l₁⊂α，l₂⊂β，α∩β=l₃，则l₁∥l₃
D．若α⊥β，α∩γ=l₁，β∩γ=l₂，则l₁∥l₂
组卷：29引用：4难度：0.8
解析
7．已知从甲袋内摸出1个红球的概率是
1
3
，从乙袋内摸出1个红球的概率是
1
2
，从两袋内各摸出1个球，则
2
3
等于（　　）
A．2个球不都是红球的概率
B．2个球都是红球的概率
C．2个球中至少有1个红球的概率
D．2个球中恰好有1个红球的概率
组卷：215引用：6难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：（本大题共6小题，满分70分）解答须写出文字说明、证明过程和演算步骤

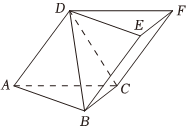21．如图，在斜三棱柱ABC-DEF中，△ABC是边长为2的正三角形，BD=CD=
4
3
3
，侧棱AD与底面ABC所成角为60°．
（1）求三棱柱ABC-DEF的体积；
（2）在线段DF（含端点）上是否存在点G，使得平面GBC与平面ABC的夹角为60°？若存在，请指出点G的位置；若不存在，请说明理由．
组卷：86引用：3难度：0.5
解析
22．已知椭圆Γ：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的右焦点为F（c,0）（c＞0），离心率为
3
2
，经过F且垂直于x轴的直线交Γ于第一象限的点M，O为坐标原点，且|OM|=
13
2
．
（Ⅰ）求椭圆Γ的方程；
（Ⅱ）设不经过原点O且斜率为
1
2
的直线交椭圆Γ于A，B两点，A，B关于原点O对称的点分别是C，D，试判断四边形ABCD的面积有没有最大值．若有，请求出最大值；若没有，请说明理由．
组卷：324引用：10难度：0.6
解析