当前位置：试卷中心 > 试卷详情

2023-2024学年福建省福州市闽侯一中高二（上）月考数学试卷（10月份）

发布：2024/9/14 0:0:8

一、单项选择题：本大题共8小题，每小题5分，共40分．在每题给出的四个选项中，只有一项是最符合题意的．

1．在空间直角坐标系中，点A（1，-3，5）关于平面yOz对称点的坐标为（　　）
A．（-1，-3，5） B．（1，3，5） C．（-1，3，-5） D．（1，3，-5）
组卷：43引用：2难度：0.8
解析
2．直线l₁，l₂的斜率是方程x²-mx-1=0的两个根，则（　　）
A．l₁∥l₂
B．l₁⊥l₂
C．l₁与l₂相交但不垂直
D．l₁与l₂的位置关系不确定
组卷：75引用：5难度：0.8
解析
3．在空间直角坐标系中，已知A（1，2，3），B（-2，-1，6），C（3，2，1），D（4，3，0），则直线AB与CD的位置关系是（　　）
A．垂直 B．平行
C．异面 D．相交但不垂直
组卷：444引用：10难度：0.7
解析
4．若
{
a
，
b
，
c
}
构成空间的一个基底，则下列向量能构成空间的一个基底的是（　　）
A．
b
+
c
，
b
，
b
-
c
B．
a
+
b
，
a
-
b
，
c
C．
a
，
a
+
b
，
a
-
b
D．
a
+
b
，
a
+
b
+
c
，
c
组卷：335引用：6难度：0.7
解析
5．已知A（-2，0），B（4，a）两点到直线l：3x-4y+1=0的距离相等，则a=（　　）
A．2 B．
9
2
C．2或-8 D．2或
9
2
组卷：1476引用：25难度：0.8
解析
6．已知直线l₁：3x+ay+1=0，l₂：（a+2）x+y+a=0．当l₁∥l₂时，a的值为（　　）
A．1 B．-3 C．-3或1 D．
-
3
2
组卷：254引用：18难度：0.8
解析
7．直线l的方向向量为
m
=
（
1
，-
1
，
0
）
，且l过点A（1，1，2），则点P（2，-2，1）到直线l的距离为（　　）
A．
2
B．
3
C．
6
D．
2
2
组卷：234引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，第17题10分，第18-22题，每题12分，共70分．解答应写出文字说明、证明过程或演算步骤．

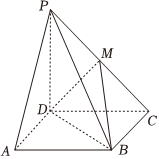21．如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，PD⊥平面ABCD，DA=DC=DP=2，点M在棱PC上，且PA∥平面BDM．
（1）求证：M是棱PC的中点；
（2）再从条件①、条件②这两个条件中选择一个作为已知，求：
（i）二面角M-BD-C的余弦值；
（ii）在棱PA上是否存在点Q，使得BQ⊥平面BDM？若存在，求出
PQ
PA
的值；若不存在，说明理由．
条件①：∠BAD=60°；
条件②：BD=2．
组卷：19引用：2难度：0.4
解析
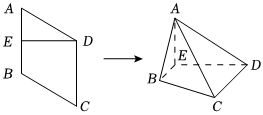22．如图，菱形ABCD的边长为2，∠BAD=60°，E为AB的中点．将△ADE沿DE折起，使A到达A'，连接A'B，A'C，得到四棱锥A'-BCDE．
（1）证明：DE⊥A'B．
（2）当二面角A'-DE-B在[
π
3
，
2
π
3
]内变化时，求直线A'C与平面A'DE所成角的正弦的最大值．
组卷：100引用：10难度：0.5
解析