2022-2023学年安徽省安庆市桐城市龙河初级中学九年级（上）第二次段测数学试卷

一、选择题

• 1．如果将抛物线y=ax²+bx+c向右平移2个单位，再向上平移3个单位，得到新的抛物线y=x²-2x+1，那么（　　）

  A．b=6，c=12

  B．b=-6，c=6

  C．b=2，c=-2

  D．b=2，c=4
  组卷：376引用：8难度：0.7

  解析

• 2．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（　　）

  A．

  B．

  C．

  D．
  组卷：5482引用：280难度：0.9

  解析

• 3．某工厂2015年产品的产量为100吨，该产品产量的年平均增长率为x（x＞0），设2015，2016，2017这三年该产品的总产量为y吨，则y关于x的函数关系式为（　　）

  A．y=100（1-x）2

  B．y=100（1+x）

  C．y= 100 （ 1 + x ） 2

  D．y=100+100（1+x）+100（1+x）2
  组卷：719引用：3难度：0.7

  解析

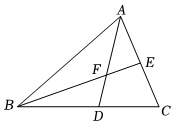• 4．如图，BE是△ABC的中线，点F在BE上，延长AF交BC于点D，若BF=3EF，则

  BD

  DC

  =（　　）

  A． 4 3

  B． 3 2

  C． 6 5

  D． 2 3
  组卷：1652引用：8难度：0.7

  解析

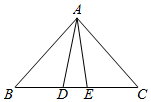• 5．古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G将一线段MN分为两线段MG，GN，使得其中较长的一段MG是全长MN与较短的一段GN的比例中项，即满足

  MG

  MN

  =

  GN

  MG

  =

  5

  -

  1

  2

  ，后人把

  5

  -

  1

  2

  这个数称为“黄金分割”数，把点G称为线段MN的“黄金分割”点．如图，在△ABC中，已知AB=AC=3，BC=4，若D，E是边BC的两个“黄金分割”点，则△ADE的面积为（　　）

  A．10-4 5

  B．3 5 -5

  C． 5 - 2 5 2

  D．20-8 5
  组卷：1901引用：24难度：0.6

  解析

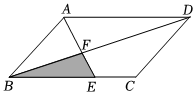• 6．如图，在平行四边形ABCD中，E是BC边上的点且BE：EC=2：1，AE、BD交于点F，设△BEF的面积为S₁，平行四边形ABCD的面积为S₂，则S₁：S₂的值为（　　）

  A． 1 16

  B． 4 15

  C． 1 5

  D． 2 15
  组卷：14引用：3难度：0.5

  解析

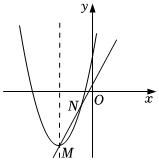• 7．如图，已知抛物线y=x²+4x+2，过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N（-1，-1），若要在y轴上找一点P，使得PM+PN最小，则点P的坐标为（　　）

  A．（0，-2）

  B． （ 0 ，- 4 3 ）

  C． （ 0 ，- 5 3 ）

  D． （ 0 ，- 5 4 ）
  组卷：33引用：2难度：0.5

  解析

三、解答题

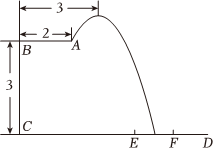• 22．2016年里约奥运会，中国跳水队赢得8个项目中的7块金牌，优秀成绩的取得离不开艰辛的训练．某跳水运动员在进行跳水训练时，身体（看成一点）在空中的运动路线是如图所示的一条抛物线，已知跳板AB长为2米，跳板距水面CD的高BC为3米，训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米，现以CD为横轴，CB为纵轴建立直角坐标系．
  （1）当k=4时，求这条抛物线的解析式；
  （2）图中CE=

  19

  4

  米，CF=

  21

  4

  米，若跳水运动员在区域EF内（含点E，F）入水时才能达到训练要求，求k的取值范围．
  组卷：21引用：2难度：0.5

  解析

• 23．定义：如果三角形I能和一个直角三角形恰好能无重叠无缝隙的拼成三角形Ⅱ，且拼成的三角形Ⅱ与三角形I相似，那么我们称三角形I与该直角三角形为“伴侣三角形”．
  
  （1）如图①，△ABC中，∠ACB=90°，CD⊥AB，则△ACD与△BCD

  “伴侣三角形”；（填写“是”或“不是”）
  （2）如图②，△ABC是由△ACD与△BCD拼成的，∠BCD=90°，且△ACD与△BCD是“伴侣三角形”，若AD=1，BD=3，求BC的长；
  （3）如图③，△ABC中，∠C=90°，AC=2，BC=1，问在△ABC三边的延长线上是否存在点D使得D与A、B、C三点中的某两点所组成的三角形与△ABC是“伴侣三角形”？若存在，请直接写出AD的长，若不存在，请说明理由．
  组卷：44引用：2难度：0.5

  解析