2022-2023学年福建省漳州市华安一中高一(下)第一次月考数学试卷
发布:2024/6/23 8:0:10
一、单选题(共40分)
-
1.已知z=i3•(2+i),则z的虚部为( )
组卷:24引用:3难度:0.8 -
2.已知向量
=(1,-2),a=(x,4),且b∥a,则|b-a|=( )b组卷:180引用:12难度:0.9 -
3.在△ABC中,角A,B,C所对的边分别是a,b,c,已知a=2bcosC,则△ABC的形状是( )
组卷:401引用:15难度:0.9 -
4.函数f(x)=sinx+cos2x的图象为( )
组卷:103引用:5难度:0.7 -
5.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
组卷:1542引用:163难度:0.9 -
 6.如图,∠A'O'B'是用斜二测画法画出的∠AOB直观图,则∠AOB是( )组卷:5引用:2难度:0.8
6.如图,∠A'O'B'是用斜二测画法画出的∠AOB直观图,则∠AOB是( )组卷:5引用:2难度:0.8 -
7.已知O为△ABC的外接圆圆心,若
,则向量CA=2OA+AB,|AB|=3|OA|在方向BA上的投影向量为( )BC组卷:16引用:2难度:0.7
四、解答题(共70分
-
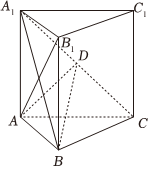 21.如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为.22
21.如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为.22
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求线段BC的长度.组卷:33引用:3难度:0.5 -
22.平行四边形ABCD中,AB=2AD=2,
,如图甲所示,作DE⊥AB于点E,将△ADE沿着DE翻折,使点A与点P重合,如图乙所示.DB=3
(1)设平面PEB与平面PDC的交线为l,判断l与CD的位置关系,并证明;
(2)当四棱锥P-BCDE的体积最大时,求二面角P-BC-D的正切值;
(3)在(2)的条件下,G、H分别为棱DE,CD上的点,求空间四边形PGHB周长的最小值.组卷:155引用:5难度:0.5


