当前位置：试卷中心 > 试卷详情

2023-2024学年河北省衡水市武强学校高二（上）开学综合素质检测数学试卷（一）

发布：2024/8/2 8:0:9

1．已知集合A={x|-2≤x≤3}，集合B满足A∩B=A，则B可能为（　　）
A．{x|-1＜x≤3} B．{x|-2＜x＜3} C．{x|-3≤x≤2} D．{x|-3≤x≤3}
组卷：145引用：3难度：0.9
解析
2．i是虚数单位，
i
3
+
3
i
=（　　）
A．
1
4
-
3
12
i B．
1
4
+
3
12
i C．
1
2
+
3
6
i
D．
1
2
-
3
6
i
组卷：142引用：18难度：0.9
解析
3．以下数据为参加数学竞赛决赛的15人的成绩：78，70，72，86，88，79，80，81，94，84，56，98，83，90，91，则这15人成绩的第80百分位数是（　　）
A．90 B．90.5 C．91 D．91.5
组卷：365引用：10难度：0.8
解析
4．函数y=a^-|x|（0＜a＜1）的图象是（　　）
A． B． C． D．
组卷：49引用：5难度：0.9
解析
5．如图，在底面为正方形，侧棱垂直于底面的四棱柱ABCD-A₁B₁C₁D₁中，AA₁=2AB=2，则异面直线A₁B与AD₁所成角的余弦值为（　　）
A．
1
5
B．
2
5
C．
3
5
D．
4
5
组卷：747引用：18难度：0.6
解析
6．已知|
a
|=3，|
b
|=2，＜
a
，
b
＞=60°，如果（3
a
+5
b
）⊥（m
a
-
b
），那么m的值为（　　）
A．
32
23
B．
23
42
C．
29
42
D．
42
23
组卷：64引用：2难度：0.7
解析
7．若角600°的终边上有一点（a,-3），则a的值是（　　）
A．-
3
B．
3
C．
3
3
D．-
3
3
组卷：127引用：3难度：0.9
解析

21．已知函数f（x）=asin2x+2cos²x-1，再从条件①、②、③这三个条件中选择一个作为已知，求：
（Ⅰ）f（x）的最小正周期；
（Ⅱ）f（x）的单调递增区间．
条件①：f（x）图象的对称轴为
x
=
π
8
；
条件②：
f
（
π
4
）
=
1
；
条件③：
a
=
3
．
组卷：187引用：4难度：0.7
解析
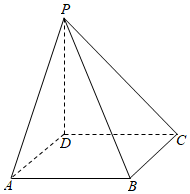22．如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l.
（1）证明：l⊥平面PDC；
（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．
组卷：7960引用：21难度：0.5
解析

1．已知集合A={x|-2≤x≤3}，集合B满足A∩B=A，则B可能为（ ）